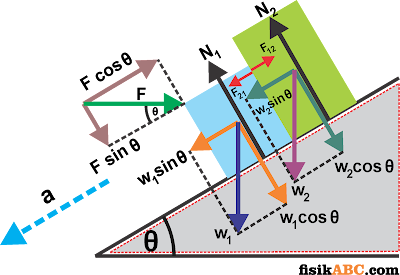
Rumus Gaya Kontak 2 balok yang Didorong Mendatar ke Atas pada Bidang Miring Licin
Daftar Materi Fisika
Dua buah benda bermassa m1 dan m2 bersentuhan di bidang miring licin, kemudian pada benda pertama diberi gaya dorong mendatar (horizontal) ke atas yang sejajar dengan permukaan alas bidang miring. Nah pada kesempatan kali ini kita akan menentukan rumus gaya kontak yang terjadi antara benda 1 dan 2. Simak penjelasan berikut ini.
Ketika benda 1 dan 2 saling bersentuhan pada bidang miring, maka benda 1 akan memberikan gaya aksi F12 kepada benda 2. Sesuai dengan hukum III Newton, benda 2 juga akan memberi gaya reaksi F21 kepada benda 1.
Pada kondisi ini terdapat 3 keadaan sistem, yaitu kedua benda akan diam, bergerak ke bawah, atau bergerak ke atas. Tentunya hal ini bergantung dengan besarnya gaya dorong F yang diberikan.
Karena terdapat 3 kondisi sistem yang berbeda tentunya rumus gaya kontak yang terjadi antara balok 1 dan 2 juga berbeda-beda. Oleh karena itu kita akan membahas cara mendapatkan rumus gaya sentuh/gaya interaksi pada masing-masing kondisi tersebut. Berikut ini uraiannya.
1. Benda Diam
Ketika sistem dalam keadaan diam, maka tidak ada percepatan yang terjadi, dengan kata lain nilai a = 0. Diagram gaya-gaya yang bekerja pada sistem ini diperlihatkan pada gambar berikut ini.
Kondisi bidang miring adalah licin sehingga tidak ada gaya gesek yang terjadi, oleh karena resultan gaya pada sumbu-Y tidak perlu diuraikan. Jadi resultan gaya yang perlu kita perhatikan hanya pada sumbu-X saja, yakni sebagai berikut:
Benda 1:
ΣFX= ma
F cos θ – w1 sin θ – F21 = m1a
F cos θ – w1 sin θ – F21 = m1(0)
F cos θ – w1 sin θ – F21 = 0
F21 = F cos θ – w1 sin θ
F21 = F cos θ – m1g sin θ ................. Pers. (1)
Benda 2:
ΣFX= ma
w2 sin θ – F12 = m2a
w2 sin θ – F12 = m2(0)
w2 sin θ – F12 = 0
F12 = w2 sin θ
F12 = m2g sin θ ................. Pers. (2)
Karena F12 = F21 maka persamaan di atas dapat kita tulis ulang sebagai berikut.
F12 = F21
m2g sin θ = F cos θ – m1g sin θ
F cos θ = m1g sin θ + m2g sin θ
F = m1g sin θ/cos θ + m2g sin θ/cos θ
F = (m1 + m2)g tan θ ................. Pers. (3)
Persamaan (3) adalah syarat nilai gaya dorong F agar kedua balok dalam kondisi diam. Perhatikan perbandingan nilai F dan (m1 + m2)g tan θ berikut ini yang menyebabkan perbedaan kondisi kedua balok.
F = (m1 + m2)g tan θ → sistem diam
F < (m1 + m2)g tan θ → sistem bergerak ke bawah
F > (m1 + m2)g tan θ → sistem bergerak ke atas
Karena tidak ada nilai percepatan, maka rumus gaya kontak untuk sistem diam adalah menggunakan persamaan (1) atau persamaan (2).
F21 = F cos θ – m1g sin θ |
Atau menggunakan rumus berikut ini.
F12 = m2g sin θ |
Keterangan: | ||
N | = | Gaya normal (N) |
w | = | Gaya berat (N) |
F | = | Gaya dorong (N) |
F12 | = | Gaya kontak benda 1 terhadap benda 2 |
F21 | = | Gaya kontak benda 2 terhadap benda 1 |
m1 | = | Massa benda 1 (kg) |
m2 | = | Massa benda 2 (kg) |
a | = | Percepatan benda (m/s2) |
g | = | Percepatan gravitasi bumi (m/s2) |
θ | = | Sudut kemiringan bidang |
F | = | Gaya dorong |
2. Benda Bergerak ke Bawah
Ketika kedua balok bergerak ke bawah, maka tentunya dalam sistem tersebut ada nilai percepatannya atau a ≠ 0. Diagram gaya-gaya yang bekerja pada sistem ini diperlihatkan pada gambar berikut ini.
Seperti pada uraian sebelumnya, langkah pertama untuk menentukan rumus gaya kontak adalah dengan menentukan resultan gaya pada sumbu-X berdasarkan Hukum II Newton yaitu sebagai berikut:
Benda 1:
ΣFX= ma
w1 sin θ + F21 – F cos θ = m1a
m1g sin θ + F21 – F cos θ = m1a
F21 = F cos θ + m1a – m1g sin θ ................. Pers. (4)
Benda 2:
ΣFX= ma
w2 sin θ – F12 = m2a
F12 = w2 sin θ – m2a
F12 = m2g sin θ – m2a ................. Pers. (5)
Karena F12 = F21 maka persamaan di atas dapat kita tulis ulang sebagai berikut.
F12 = F21
m2g sin θ – m2a = F cos θ + m1a – m1g sin θ
m1a + m2a = m1g sin θ + m2g sin θ – F cos θ
a(m1 + m2) = (m1 + m2)g sin θ – F cos θ
a = [(m1 + m2)g sin θ – F cos θ]/m1 + m2
a = (m1 + m2)g sin θ/(m1 + m2) – F cos θ/(m1 + m2)
a = g sin θ – F cos θ/(m1 + m2) ................. Pers. (6)
Dengan demikian rumus percepatan pada sistem ini adalah sebagai berikut.
a | = | g sin θ | – | F cos θ |
m1 + m2 |
Dari rumus percepatan di atas, kita dapat menentukan persamaan gaya kontak antara benda 1 dan 2 untuk sistem dalam keadaan bergerak ke bawah yaitu sebagai berikut.
F12 = m2g sin θ – m2a
F12 = m2g sin θ – m2[g sin θ – F cos θ/(m1 + m2)]
F12 = m2g sin θ – m2g sin θ + m2F cos θ/( m1 + m2)
F12 = m2F cos θ/( m1 + m2) ................. Pers. (7)
Dari persamaan (4) tersebut maka rumus gaya kontak/gaya interaksi antara benda 1 dan benda 2 adalah sebagai berikut.
F12 = F21 | = | m2F cos θ |
m1 + m2 |
Keterangan: | ||
N | = | Gaya normal (N) |
w | = | Gaya berat (N) |
F | = | Gaya dorong (N) |
F12 | = | Gaya kontak benda 1 terhadap benda 2 |
F21 | = | Gaya kontak benda 2 terhadap benda 1 |
m1 | = | Massa benda 1 (kg) |
m2 | = | Massa benda 2 (kg) |
a | = | Percepatan benda (m/s2) |
g | = | Percepatan gravitasi bumi (m/s2) |
θ | = | Sudut kemiringan bidang |
F | = | Gaya dorong |
3. Benda Bergerak ke Atas
Untuk kondisi kedua balok bergerak ke atas maka syaratnya adalah sebagai berikut:
F > (m1 + m2)g tan θ
Pada keadaan ini diagram gaya-gaya yang bekerja pada sistem diperlihatkan seperti pada gambar berikut ini.
Berdasarkan Hukum II Newton, resultan gaya di sumbu-X pada masing-masing balok adalah sebagai berikut:
Benda 1:
ΣFX= ma
F cos θ – w1 sin θ – F21 = m1a
F21 = F cos θ – w1 sin θ – m1a
F21 = F cos θ – m1g sin θ – m1a ................. Pers. (8)
Benda 2:
ΣFX= ma
F12 – w2 sin θ = m2a
F12 = m2a + w2 sin θ
F12 = m2a + m2g sin θ ................. Pers. (9)
Karena F12 = F21 maka persamaan di atas dapat kita tulis ulang sebagai berikut.
F12 = F21
m2a + m2g sin θ = F cos θ – m1g sin θ – m1a
m1a + m2a = F cos θ – m1g sin θ – m2g sin θ
a (m1 + m2) = F cos θ – (m1 + m2)g sin θ
a = [F cos θ – (m1 + m2)g sin θ]/(m1 + m2)
a = F cos θ/( m1 + m2) – (m1 + m2)g sin θ/(m1 + m2)
a = (F cos θ/ m1 + m2) – g sin θ ................. Pers. (10)
Dengan demikian rumus percepatan pada sistem ini adalah sebagai berikut.
a | = | F cos θ | – | g sin θ |
m1 + m2 |
Dari rumus percepatan di atas, kita dapat menentukan persamaan gaya kontak antara benda 1 dan 2 untuk sistem dalam keadaan bergerak ke atas yaitu sebagai berikut.
F12 = m2a + m2g sin θ
F12 = m2[(F cos θ/ m1 + m2) – g sin θ] + m2g sin θ
F12 = m2F cos θ/( m1 + m2) – m2g sin θ + m2g sin θ
F12 = m2F cos θ/( m1 + m2) ................. Pers. (11)
Dari persamaan (11) tersebut maka rumus gaya kontak/gaya interaksi antara benda 1 dan benda 2 adalah sebagai berikut.
F12 = F21 | = | m2 F cos θ |
m1 + m2 |
Keterangan: | ||
N | = | Gaya normal (N) |
w | = | Gaya berat (N) |
F | = | Gaya dorong (N) |
F12 | = | Gaya kontak benda 1 terhadap benda 2 |
F21 | = | Gaya kontak benda 2 terhadap benda 1 |
m1 | = | Massa benda 1 (kg) |
m2 | = | Massa benda 2 (kg) |
a | = | Percepatan benda (m/s2) |
g | = | Percepatan gravitasi bumi (m/s2) |
θ | = | Sudut kemiringan bidang |
F | = | Gaya dorong |
Dari perumusan di atas, ternyata gaya kontak untuk dua kondisi yaitu sistem bergerak ke bawah dan ke atas ternyata memiliki rumus yang sama dengan demikian dapat disimpulan bahwa ketika 2 balok saling bersentuhan di bidang miring licin kemudian mendapat gaya dorong horizontal ke atas, maka akan memiliki gaya kontak yang sama baik kedua balok bergerak ke bawah maupun ke atas.