Contoh Soal Gaya Gesek Pada Bidang Datar dan Miring
Daftar Materi Fisika
Gaya gesek (friction force) adalah gaya yang bekerja antara dua permukaan benda yang saling bersentuhan atau bersinggungan. Arah gaya gesek berlawanan arah dengan kecenderungan arah gerak benda. Gaya gesek disimbolkan dengan huruf f dan satuannya adalah Newton.
Nah pada kesempatan kali ini kita akan membahas tentang kumpulan contoh soal gaya gesek pada gerak benda di bidang datar dan juga bidang miring. Oleh karena itu, silahkan kalian simak baik-baik pembahasannya berikut ini.
Contoh Soal Gaya Gesek Pada Bidang Datar
1. Sebuah balok 10 kg diam di atas lantai datar. Koefisien gesekan statis μs = 0,4 dan koefisien gesek kinetis μk = 0,3. Tentukanlah gaya gesekan yang bekerja pada balok jika gaya luar F diberikandalam arah horizontal sebesar:
(a) 0 N
(b) 20 N
(c) 42 N
Penyelesaian:
Diketahui:
m = 10 kg
μs = 0,4
μk = 0,3
g = 10 m/s2
F = 0 N, 20 N dan 42 N
Ditanyakan: f?
Jawab:
Gaya-gaya yang bekerja pada benda diperlihatkan seperti pada gambar di bawah ini.
Karena pada sumbu vertikal tidak terjadi gerak, maka berdasarkan Hukum I Newton berlaku:
ΣFY = 0
N – w = 0
N = w
N = mg
N = (10 kg)(10 m/s2)
N = 100 N
(a) Gaya gesek yang bekerja pada balok jika F = 0 N
Karena gaya luar F = 0, maka benda pasti tidak bergerak sehingga gaya geseknya sama dengan nol
f = 0
Jadi, gaya gesek yang bekerja pada balok adalah 0 N.
(b) Gaya gesek yang bekerja pada balok jika F = 20 N
fs = μsN
fs = (0,4)(100 N)
fs = 40 N
Karena F < fs maka benda masih dalam keadaan diam (F = 20 N tidak cukup untuk menggerakkan benda). Oleh karena itu berlaku Hukum I Newton yaitu sebagai berikut.
ΣFX = 0
F – f = 0
f = F
f = 20 N
Jadi, gaya gesek yang bekerja pada balok adalah 20 N.
(c) Gaya gesek yang bekerja pada balok jika F = 32 N
F = 40 N > fs = 40 N maka benda bergerak. Karena benda bergerak, maka gaya gesek yang bekerja adalah gaya gesek kinetis yaitu sebesar:
fk = μkN
fk = (0,3)(100)
fk = 30 N
Jadi, gaya gesek yang bekerja pada balok adalah 30 N.
2. Sebuah balok bermassa 20 kg berada di atas lantai mendatar kasar. μs = 0,6 dan μk = 0,3. Kemudian balok ditarik gaya sebesar F mendatar. g = 10 m/s2. Tentukan gaya gesek yang dirasakan balok dan percepatan balok jika:
(a) F = 100 N
(b) F = 140 N
Penyelesaian:
Diketahui:
m = 20 kg
μs = 0,6
μk = 0,3
g = 10 m/s2
F = 100 N dan 140 N
Ditanyakan: f dan a?
Jawab:
Gambar diagram gaya yang bekerja pada balok sama seperti pada gambar contoh soal nomor 1 di atas. Gaya normal N memenuhi:
N = w = mg = (20 kg)(10 m/s2) = 200 N
Pengaruh gaya F dapat diketahui dengan menghitung dahulu gaya gesek statis yang bekerja pada balok, yaitu sebagai berikut.
fs = μsN
fs = (0,6)(200 N)
fs = 120 N
(a) Untuk F = 100 N
Karena F < fs maka balok masih tetap diam sehingga berlaku Hukum I Newton yaitu sebagai berikut.
ΣFX = 0
F – f = 0
f = F
f = 100 N
Karena benda diam, maka a = 0
Jadi, gaya gesek dan percepatan balok sebesar 100 N dan 0 m/s2.
(b) Untuk F = 140 N
F > fs maka balok bergerak dan gaya gesek yang bekerja adalah gaya gesek kinetik, yaitu sebesar:
fk = μkN
fk = (0,3)(200)
fk = 60 N
Karena balok bergerak, maka berlaku Hukum II Newton yaitu sebagai berikut.
ΣFX = ma
F – fk = ma
140 – 60 = 20a
20a = 80
a = 4 m/s2
Jadi, gaya gesek dan percepatan balok adalah 60 N dan 4 m/s2.
3. Sebuah balok dengan massa 2 kg terletak di atas lantai mendatar. Balok tersebut ditarik oleh gaya 4 N ke atas membentuk sudut 60o terhadap arah mendatar. Bila percepatan gravitasi g = 10 m/s2, koefisien gesek kinetis antara balok dan lantai 0,1. Sedangkan koefisien gesek statisnya 0,2. Maka gaya gesek yang bekerja pada balok dan lantai sebesar…
Penyelesaian:
Diketahui:
m = 2 kg
F = 4 N
θ = 60o
g = 10 m/s2
μk = 0,1
μs = 0,2
Ditanyakan: f?
Jawab:
Diagram gaya-gaya yang bekerja pada balok diperlihatkan seperti pada gambar berikut ini.
■ Gaya Normal
Karena pada sumbu vertikal tidak terjadi gerak, maka berdasarkan Hukum I Newton berlaku:
ΣFY = 0
N + F sin θ – w = 0
N = w – F sin θ
N = mg – F sin θ
N = (2 kg)(10 m/s2) – (4 N)(sin 60o)
N = 20 N – (4 N)(1/2 √3)
N = 20 N – 2√3 N
N = 16,6 N
■ Gaya Gesek Statis
fs = μsN
fs = (0,2)(15,6)
fs = 3,32 N
■ Gaya Tarik
Gaya yang bekerja segaris dengan gaya gesek adalah komponen gaya F dalam arah mendatar yaitu F cos θ. Untuk mengetahui apakah balok bergerak atau tidak, maka kita hitung komponen gaya tersebut, yaitu sebagai berikut.
FX = F cos θ
FX = (4)(cos 60o)
FX = (4)(1/2)
FX = 2 N
■ Kesimpulan
FX < fs berarti balok masih dalam keadaan diam. Oleh karena itu, resultan gaya dalam arah sumbu-X memenuhi Hukum I Newton, yaitu sebagai berikut.
ΣFX = 0
FX – fs = 0
fs = FX
fs = 2 N
Jadi, gaya gesek yang bekerja pada balok dan lantai sebesar 2 N.
4. Pada susunan benda-benda seperti gambar di bawah ini.
K adalah katrol, m1 = 10 kg, m2 = 5 kg, m3 = 10 kg, koefisien gesekan antara m1 dan m2 adalah 0,2 sedangkan koefisien gesekan antara m2 dengan bidang adalah 0,4. Apabila beban m3 dilepas, maka:
(a) Hitung gaya gesekan antara m1 dan m2
(b) Hitung gaya gesekan antara m2 dan bidang
Penyelesaian:
Pertama, kita lukis garis-garis gaya yang bekerja pada sistem, seperti yang diperlihatkan pada gambar berikut ini.
(a) Gaya gesekan antara m1 dan m2 adalah sebagai berikut
Untuk benda m1, dalam arah vertikal berlaku Hukum I Newton yaitu sebagai berikut.
ΣFY = 0
N1 – w1 = 0
N1 = w1
N1 = m1g
Maka gaya geseknya adalah sebagai berikut.
f1 = μ1N1
f1 = μ1m1g
f1 = (0,2)(10 kg)(10 m/s2)
f1 = 20 N
(b) Gaya gesekan antara m2 dan bidang adalah sebagai berikut.
Untuk benda m2, dalam arah vertikal juga berlaku Hukum I Newton, yaitu sebagai berikut.
ΣFY = 0
N1 + N2 – w1 – w2 = 0
N1 + N2 = w1 + w2
N1 + N2 = m1g + m2g
Maka gaya geseknya adalah sebagai berikut.
f2 = μ2(N1 + N2)
f2 = μ2(m1g + m2g)
f2 = μ2(m1 + m2)g
f2 = (0,4)(10 + 5)(10)
f2 = (0,4)(15)(10)
f2 = 60 N
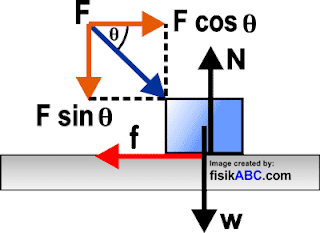
5. Sebuah peti bermassa 50 kg, mula-mula diam di atas lantai horizontal kasar (μk = 0,1; μs = 0,5). Kemudian peti itu didorong dengan gaya F = 100 N yang arahnya membentuk sudut θ terhadap arah horizontal. Jika sin θ = 0,6 dan cos θ = 0,8. Gaya gesek yang dialaminya sebesar…
Penyelesaian:
Diketahui:
m = 50 kg
μk = 0,1
μs = 0,5
F = 100 N
sin θ = 0,6
cos θ = 0,8
g = 10 m/s2
Ditanyakan: f?
Jawab:
Diagram gaya yang bekerja pada benda tersebut diperlihatkan seperti pada gambar di bawah ini.
Dalam arah vertikal tidak terjadi gerak (diam) sehingga berlaku Hukum I Newton yaitu sebagai berikut.
ΣFY = 0
N – F sin θ – w = 0
N = F sin θ + w
N = F sin θ + mg
Gaya gesek statis benda adalah sebagai berikut.
fs = μsN
fs = μs(F sin θ + mg)
fs = (0,5)[(100)(0,6) + (50)(10)]
fs = (0,5)(60 + 500)
fs = (0,5)(560)
fs = 280 N
Karena F < fs maka benda diam sehingga berlaku Hukum I Newton yaitu sebagai berikut.
ΣFX = 0
F cos θ – f = 0
f = F cos θ
f = (100)(0,8)
f = 80 N
Dengan demikian, gaya gesek yang dialami peti tersebut sebesar 80 N.
6. Sebuah balok bermassa m1 ditumpuk di atas balok yang massanya m serta berada di atas lantai horizontal yang licin, seperti yang ditunjukkan pada gambar di bawah ini.
Kemudian, sebuah gaya F dikerjakan pada balok 2. Koefisien gesekan statis dan kinetis antara balok-balok adalah μs dan μk.
∎ Tentukanlah nilai maksimum F supaya balok tidak bergerak satu sama lainnya.
∎ Tentukanlah percepatan setiap balok jika F lebih besar daripada nilai tersebut.
Jawab
Langkah pertama untuk menjawab soal fisika yang berkaitan dengan dinamika adalah dengan menggambarkan diagram gaya yang bekerja pada sistem. Untuk soal di atas, karena terdapat dua benda maka untuk mempermudah memahami gaya-gaya yang bekerja secara spesifik, kita gambarkan diagram gaya kedua benda secara terpisah. Perhatikan gambar di bawah ini.
Perhatikan gambar diagram gaya pada kedua balok di atas. Pada balok 1, bekerja tiga gaya yaitu gaya normal, gaya berat dan gaya gesek. Gaya gesek pada balok 1 timbul karena permukaan balok 1 dan 2 saling bersentuhan. Sedangkan pada balok 2 bekerja empat gaya, yaitu gaya normal, gaya berat, gaya gesek dan gaya tarik F. Gaya gesek yang sama juga bekerja pada balok 2 tetapi dengan arah yang berlawanan.
∎ F maksimum agar balok 1 tidak bergerak
Syarat agar balok 1 tidak bergerak terhadap balok 2 maka percepatan balok 1 harus sama dengan percepatan balok 2.
a1 = a2
Kemudian kita tinjau resultan gaya yang bekerja pada masing-masing balok dengan menggunakan Hukum I dan II Newton sebagai berikut.
Tinjau balok 1
ΣFY = 0
N1 – w1 = 0
N1 = w1
N1 = m1g
ΣFX = ma
f = m1a1
Karena balok 1 tidak bergerak maka gaya gesek yang bekerja adalah gaya gesek statis.
fs = m1a1
μsN1 = m1a1
μsm1g = m1a1
a1 = μsg ………………. Pers. (1)
Tinjau balok 2
ΣFX = ma
F – f = m2a2
F – μsm1g = m2a2 ………………. Pers. (2)
Karena a1 = a2 maka persamaan (1) dapat kita subtitusikan ke dalam persamaan (2) sebagai berikut.
F – μsm1g = m2(μsg)
F – μsm1g = μsm2g
F = μsm1g + μsm2g
F = μsg(m1 + m2)
Dengan demikian, nilai F maksimum agar balok tidak bergerak satu sama lainnya adalah F = μsg(m1 + m2).
∎ Percepatan balok 1 dan 2
Apabila nilai F > μsg(m1 + m2) maka balok 1 akan bergerak terhadap balok 2. Karena bergerak, maka gaya gesek yang bekerja adalah gaya gesek kinetis. Lalu untuk menentukan besar percepatan masing-masing balok, kita gunakan persamaan Hukum II Newton sebagai berikut.
Tinjau balok 1
ΣFX = ma
fk = m1a1
μkm1g = m1a1
a1 = μkm1g
jadi besar percepatan balok 1 adalah a1 = μkm1g
Tinjau balok 2
ΣFX = ma
F – fk = m2a2
F – μkm1g = m2a2
a2 = (F – μkm1g)/m2
jadi besar percepatan balok 2 adalah a2 = (F – μkm1g)/m2
7. Balok A = 15 kg dan balok B = 20 kg ditumpuk seperti pada gambar di bawah ini. Koefisien gesek kinetik antara balok A dengan balok B dan balok B dengan lantai sama yaitu μk = 0,3. Jika balok B ditarik gaya F sehingga bergerak pelan maka tentukan perbandingan gaya gesek yang bekerja antara balok A dan B dengan gaya gesek yang bekerja antara balok B dan lantai.
Jawab
Diketahui:
mA = 15 kg
mB = 20 kg
μk = 0,3
g = 10 m/s2
F = undefine
Ditanyakan: fA : fB
Seperti pada soal sebelumnya, langkah pertama kita gambarkan diagram gaya secara terpisah antara balok A dan balok B seperti yang diperlihatkan pada gambar di bawah ini.
Perhatikan gambar diagram gaya yang bekerja pada kedua balok di atas. Gaya gesek yang bekerja antara balok A dengan balok B adalah fA sedangkan gaya gesek yang bekerja antara balok B dengan lantai adalah fB. Besar masing-masing gaya gesek tersebut adalah sebagai berikut.
fA = μkNA
fA = μkwA
fA = μkmAg
fA = (0,3)(15)(10)
fB = 45 N
fB = μkNAB
fB = μk(wA + wB)
fB = μk(mAg + mBg)
fB = 0,3[(15 × 10) + (20 × 10)]
fB = 0,3(150 + 200)
fB = 0,3(350)
fB = 105 N
Dengan demikian, perbandingan gaya gesek antara balok A dan balok B dengan gaya gesek antara balok B dengan lantai adalah sebagai berikut.
fA : fB = 45 N : 105 N
fA : fB = 3 : 7
8. Koefisien gesek statis antara sebuah lemari kayu dengan lantai kasar suatu bak mobil pick up sebesar 0,75. Berapakah percepatan maksimum yang masih boleh dimiliki mobil agar lemari tetap tak bergerak terhadap bak truk tersebut?
Jawab
Diketahui:
μs = 0,75
g = 10 m/s2
Ditanyakan: Percepatan maksimum (amaks)
Pertama, kita gambarkan ilustrasi kejadian pada soal tersebut. Kemudian lukiskan garis-garis gaya yang bekerja pada objek seperti yang diperlihatkan pada gambar di bawah ini.
Perhatikan diagram gaya yang bekerja pada lemari di atas. Dengan menggunakan Hukum II Newton, kita peroleh persamaan gerak lemari sebagai berikut.
ΣFX = ma
f = mamaks
μsN = mamaks
μsmg = mamaks
μsmg = mamaks
amaks = μsg
amaks = (0,75)(10)
amaks = 7,5 m/s2
jadi kecepatan maksimum mobil pick up tersebut agar lemari tetap dalam keadaan diam adalah sebesar 7,5 m/s2.
9. Sebuah buku bermassa 300 g diletakkan di atas meja. Jika buku diberi gaya luar sebesar 0,5 N dan koefisien gesekan statis antara buku dengan permukaan meja 0,2; berapakah gaya gesek statis maksimum yang terjadi antara buku dengan permukaan meja, dan apakah buku dapat bergerak? (g = 10 m/s2).
Penyelesaian:
Diketahui:
m = 300 g = 0,3 kg
F = 0,5 N
g = 10 m/s2
μs = 0,2
Ditanyakan: fs maks
Jawab:
Untuk mempermudah dalam pengerjaan soal, kita gambarkan objek beserta diagram gayanya seperti yang diilustrasikan pada gambar berikut ini.
Berdasarkan Hukum II Newton, maka resultan gaya yang bekerja pada sumbu-Y adalah sebagai berikut.
ΣFY = ma
Karena buku tidak bergerak dalam arah vertikal maka a = 0 sehingga:
ΣFY = 0
N – w = 0
N = w
N = mg ……………...… Pers. (a)
Untuk mencari gaya gesek statis, kita dapat menggunakan persamaan:
fs maks = μsN ………… Pers. (b)
masukkan nilai N pada persamaan (a) ke persamaan (b) sehingga diperoleh:
fs maks = μsmg
fs maks = 0,2 × 0,3 × 10
fs maks = 0,6 N
Jadi, besarnya fs maks adalah 0,6 N. Karena fs maks > F, maka buku tidak bergerak alias diam.
10. Seorang siswa mendorong balok kayu yang beratnya 40 N di atas lantai. Koefisien gesekan statik antara balok dengan lantai (μs) adalah 0,5 dan koefisien gesek kinetik (μk) 0,3. Tentukan:
■ Besar gaya yang diberikan siswa tersebut agar balok tepat akan bergerak.
■ Gaya gesek balok dengan lantai pada saat balok diam.
■ Gaya yang diberikan siswa, jika balok bergerak dengan percepatan 2,5 m/s2 dan percepatan gravitasi 10 m/s2
Penyelesaian:
Diketahui:
w = 40 N
μs = 0,5
μk = 0,3
Ditanyakan:
a) F agar benda tepat akan bergerak
b) fs dan fk
c) F jika a = 0,5 m/s2
Jawab:
Gaya-gaya yang bekerja pada balok tersebut dapat digambarkan sebagai berikut.
Dari gambar diagram gaya yang bekerja pada balok di atas, maka kita ketahui bahwa gaya normal sama dengan gaya berat balok.
N = w = 40 N
■ Agar balok tepat akan bergerak maka:
F = fs maks
F = μsN
F = (0,5)(40)
F = 20 N
Jadi, gaya yang harus diberikan agar balok tepat akan bergerak adalah 20 Newton.
■ Pada saat balok diam, gaya gesek yang bekerja adalah gaya gesek statis, yaitu sebesar 20 N.
■ Pada saat bergerak, gaya gesek yang bekerja adalah gaya gesek kinetis.
fk = μkN
fk = (0,3)(40)
fk = 12 N
Dengan demikian, gaya total yang bekerja pada balok ditentukan dengan menggunakan persamaan Hukum II Newton, yaitu sebagai berikut.
ΣFx = ma
F – fk = ma
F = ma + fk
F = (w/g)a + fk
F = (40/10)(2,5) + 12
F = (4)(2,5) + 12
F = 10 + 12
F = 22 N
Jadi, gaya yang diberikan siswa pada balok adalah 22 Newton.
Contoh Soal Gaya Gesek Pada Bidang Miring
1. Sebuah benda yang beratnya w meluncur ke bawah dengan kecepatan tetap pada suatu bidang miring yang kasar. Bidang miring tersebut membentuk sudut 37o dengan arah horizontal. Hitung koefisien gesekan antara benda dengan bidang tersebut.
Penyelesaian:
Pertama kita gambarkan diagram gaya yang bekerja pada benda tersebut, seperti yang diperlihatkan pada gambar di bawah ini.
Benda bergerak dengan kecepatan tetap, hal ini berarti benda melakukan gerak lurus beraturan (GLB) sehingga percepatannya adalah nol (a = 0).
■ Pada sumbu-Y, berlaku Hukum I Newton, yaitu sebagai berikut.
ΣFY = 0
N – w cos θ = 0
N = w cos θ
N = mg cos θ
■ Pada sumbu-X, berlaku Hukum II Newton, yaitu sebagai berikut.
ΣFX = ma
w sin θ – f = m(0)
mg sin θ – μkN= 0
mg sin θ – μkmg cos θ = 0
μkmg cos θ = mg sin θ
μk cos θ = sin θ
μk = sin θ/cos θ
μk = tan θ
μk = tan 37o
μk = 0,75
Jadi, koefisien gesekan antara benda dengan bidang adalah 0,75.
2. Sebuah balok bergerak menuruni bidang yang kemiringannya 30o terhadap bidang horizontal. Jika balok bergerak dengan percepatan 4 m/s2, tentukanlah koefisien gesek kinetis antara balok dengan bidang.
Penyelesaian:
Diagram gaya yang bekerja pada balok sama seperti pada soal nomor 1 di atas. Karena balok memiliki percepatan, maka balok melakukan gerak lurus berubah beraturan (GLBB).
■ Pada sumbu-Y, berlaku Hukum I Newton, yaitu sebagai berikut.
ΣFY = 0
N – w cos θ = 0
N = w cos θ
N = mg cos θ
■ Pada sumbu-X, berlaku Hukum II Newton, yaitu sebagai berikut.
ΣFX = ma
w sin θ – f = ma
mg sin θ – μkN= ma
mg sin θ – μkmg cos θ = ma
μkmg cos θ = mg sin θ – ma
μkg cos θ = g sin θ – a
μk(10)(cos 30o)= (10)(sin 30o) – 4
μk(10)(0,866)= (10)(0,5) – 4
8,66μk = 5 – 4
8,66μk = 1
μk = 1/8,66
μk = 0,12
Jadi, koefisien gesekan antara benda dengan bidang adalah 0,12.
3. Sebuah benda dengan berat 30 N berada pada bidang miring. Ternyata, benda tepat akan meluncur ke bawah. Jika percepatan gravitasi bumi adalah 10 m/s2, tentukan koefisien gesek antara benda dengan bidang miring!
Penyelesaian:
Dari soal kita ketahui bahwa benda tepat akan meluncur jadi benda belum bergerak, sehingga gaya gesek yang bekerja adalah gaya gesek statis. Untuk menentukan koefisien gesek (statis), kita gunakan rumus seperti yang telah diuraikan pada soal nomor 1 di atas, yaitu sebagai berikut.
μs = tan θ
μs = tan (30o)
μs = 1/3 √3
Lalu bagaimana jika kita lupa dengan rumus koefisien gesek tersebut? Tenang saja, bagi kalian yang tidak suka menghafal rumus, masih ada metode manual untuk menyelesaikan persoalan di atas. Metode manual yang dimaksud adalah dengan menentukan persamaan gerak benda berdasarkan Hukum Newton. Langkah pertama adalah menggambar garis-garis gaya yang bekerja pada benda, yaitu sebagai berikut.
Resultan gaya pada sumbu-Y adalah sebagai berikut.
ΣFY = 0
N – w cos 30o = 0
N = w cos 30o
Karena benda belum bergerak, maka a = 0. Sehingga berlaku Hukum I Newton pada sumbu-X yaitu sebagai berikut.
ΣFX = 0
w sin 30o – fs = 0
w sin 30o – μsN = 0
μsN = w sin 30o
μsw cos 30o = w sin 30o
μs cos 30o = sin 30o
μs | = | sin 30o |
cos 30o | ||
μs | = | ½ |
½ √3 |
μs = 1/3 √3
Jadi, koefisien gesek antara benda dengan bidang miring adalah 1/3 √3.