Contoh Soal Gaya Tegangan Tali dan Pembahasan
Daftar Materi Fisika
Gaya tegangan tali atau tension force adalah gaya pada tali ketika tali tersebut dalam keadaan tegang. Gaya tegangan tali dilambangkan dengan huruf T kapital dan satuannya adalah Newton. Arah gaya tegangan tali bergantung pada titik atau benda yang ditinjau. Dalam pelajaran fisika, terdapat beberapa kasus gaya tegangan tali pada gerak benda-benda yang dihubungan tali, secara umum terdapat beberapa kondisi yaitu:
■ Gaya tegangan tali pada sistem bidang datar licin
■ Gaya tegangan tali pada sistem bidang datar kasar
■ Gaya tegangan tali pada sistem bidang miring licin
■ Gaya tegangan tali pada sistem bidang miring kasar
Nah pada kesempatan kali ini kita akan membahas beberapa contoh soal tentang menentukan besar gaya tegangan tali pada sistem bidang datar dan miring baik dengan kondisi licin maupun kasar, oleh karena itu silahkan kalian simak baik-baik pembahasan berikut ini.
1. Gambar di bawah ini menunjukkan tiga buah balok yaitu A, B dan C yang terletak di bidang mendatar licin. Jika massa A = 5 kg, massa B = 3 kg dan massa C = 2 kg dan F = 10 N, maka tentukan perbandingan besar tegangan tali antara A dan B dengan besar tegangan tali antara B dan C.

Jawab
Diketahui:
mA = 5 kg
mB = 3 kg
mC = 2 kg
F = 10 N
Ditanyakan: Perbandingan tegangan tali AB (TAB) dengan tegangan tali BC (TBC)
Pertama, seperti biasa kita gambarkan terlebih dahulu diagram gaya yang bekerja pada sistem seperti yang terlihat pada gambar berikut ini.

Untuk menentukan tegangan tali antara A dan B serta tegangan tali antara B dan C, kita harus menentukan terlebih dahulu besar percepatan ketiga balok. Caranya adalah dengan meninjau gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.
∎ Tinjau balok A
ΣFX = ma
TAB = mAa ……………...… Pers. (4.1)
∎ Tinjau balok B
ΣFX = ma
TBC – TAB = mBa ……….… Pers. (5.1)
Subtitusikan persamaan (4) ke dalam persamaan (5.1)
TBC – mAa = mBa
TBC = mAa + mBa ……..… Pers. (6.1)
∎ Tinjau balok C
ΣFX = ma
F – TBC = mCa ….……..… Pers. (7.1)
Subtitusikan persamaan (6.1) ke dalam persamaan (7.1)
F – (mAa + mBa) = mCa
F = mAa + mBa + mCa
F = (mA + mB + mC)a
a = F/(mA + mB + mC) ………. Pers. (8.1)
Kemudian kita memasukkan nilai-nilai yang diketahui dari soal ke persamaan (8.2), sehingga akan kita peroleh besar percepatan ketiga balok sebagai berikut.
a = 10/(5 + 3 + 2)
a = 10/10
a = 1 m/s2
Langkah selanjutnya adalah menentukan TAB dan TBC dengan memasukkan nilai percepatan tersebut ke persamaan (4.1) dan (5.1) sebagai berikut.
TAB = mAa
TAB = (5)(1)
TAB = 5 N
TBC – TAB = mBa
TBC – 5= (3)(1)
TBC = 3 + 5
TBC = 8 N
Dengan demikian perbandingan besar tegangan tali antara A dan B dengan besar tegangan tali antara B dan C adalah sebagai berikut.
TAB : TBC = 5 : 8
2. Balok A yang bermassa 3 kg diletakkan di atas meja kemudian diikat tali yang menghubungkan balok B dengan massa 2 kg melalui sebuah katrol seperti yang diperlihatkan pada gambar di bawah ini. Massa dan gesekan katrol diabaikan sedangkan percepatan gravitasi g = 10 m/s2. Tentukanlah besar percepatan sistem dan tegangan tali jika meja licin.

Penyelesaian:
Diketahui:
mA = 3 kg
mB = 2 kg
g = 10 m/s2
untuk meja kasar, μk = 0,4
Ditanyakan: Percepatan dan gaya tegangan tali.
Jawab:
Hal utama yang perlu kita lakukan adalah menggambarkan diagram atau garis-garis gaya yang bekerja pada sistem. Gambar diagram gayanya adalah sebagai berikut.

Dari gambar diagram gaya di atas, maka kita dapat menentukan resultan gaya pada masing-masing balok. Untuk balok B yang menggantung tentu saja tidak ada resultan gaya pada sumbu-X sedangkan pada balok A, kita tidak perlu menguraikan resultan gaya pada sumbu-Y dikarenakan tidak terdapat gaya gesek. Dengan menggunakan Hukum II Newton, maka resultan gaya masing-masing benda adalah sebagai berikut.
Tinjau Balok A
ΣFX = ma
T = mAa …………… Pers. (1.2)
Tinjau Balok B
ΣFY = ma
wB – T = mBa
mBg – T = mBa …………… Pers. (2.2)
Subtitusikan persamaan (1.2) ke persamaan (2.2)
mBg – T = mBa
mBg – mAa = mBa
mAa + mBa = mBg
(mA + mB)a = mBg
a = mBg/(mA + mB) …………… Pers. (3.2)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (3.2)
a = (2)(10)/(3 + 2)
a = 20/5
a = 4 m/s2
Jadi besar percepatan sistem untuk keadaan meja licin adalah 4 m/s2. Untuk menentukan besar gaya tegangan tali, kita masukkan nilai percepatan ke persamaan (1.2) sebagai berikut.
T = mAa
T = (3)(4)
T = 12 N
Jadi besar gaya tegangan tali untuk kondisi meja licin adalah 12 N.
3. Dua balok yaitu balok m1 dan balok m2 dihubungkan dengan seutas tali melalui dua katrol. Balok m1 terletak pada bidang datar dan dihubungkan pada katrol tetap sedangkan balok m2 dihubungkan pada katrol bebas bergerak seperti yang diperlihatkan pada gambar di bawah ini.

Pada rangkaian seperti pada gambar di atas, massa balok 1 dan 2 masing-masing adalah 3 kg dan 4 kg. Kedua katrol licin serta massa tali dan katrol diabaikan (g = 10 m/s2). Tentukanlah percepatan masing-masing balok dan gaya tegangan tali sistem apabila Bidang datar kasar dengan koefisien gesek kinetis 0,25.
Penyelesaian
Diketahui:
m1 = 3 kg
m2 = 4 kg
μk = 0,25 (bidang kasar)
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab:
Sebelum dapat menentukan resultan gaya baik pada balok 1 maupun balok 2, tentunya kita harus menggambarkan diagram gaya yang bekerja pada sistem terlebih dahulu. Perhatikan gambar berikut ini.

Tinjau Balok 1
ΣFY = ma
N – w1 = m1a1
N – m1g = m1a1
Karena tidak terjadi gerak dalam arah sumbu-Y, maka a = 0 sehingga
N – m1g = 0
N = m1g
ΣFX = ma
T – f = m1a1
T – μkN = m1a1
Karena N = m1g maka
T – μkm1g = m1a1
T = m1a1 + μkm1g …………… Pers. (6.3)
Tinjau Balok 2
ΣFY = ma
w2 – 2T = m2a2
m2g – 2T = m2a2 …………… Pers. (7.3)
Subtitusikan persamaan (6.3) ke dalam persamaan (7.3)
m2g – 2(m1a1 + μkm1g) = m2a2
2m1a1 + m2a2 = m2g – 2μkm1g
Karena a1 = 2a2 maka
2m1(2a2) + m2a2 = m2g – 2μkm1g
4m1a2 + m2a2 = m2g – 2μkm1g
(4m1 + m2)a2 = (m2 – 2μkm1)g
a2 = (m2 – 2μkm1)g/(4m1 + m2) …………… Pers. (8.3)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (8.3)
a2 = [4 – 2(0,25)(3)]10/[4(3) + 4]
a2 = (4 – 1,5)10/(12 + 4)
a2 = (2,5)10/16
a2 = 1,56 m/s2
Karena a2 = 1,56 maka a1 = 2 × 1,56 = 3,12 m/s2
Jadi, Untuk kondisi bidang datar kasar, besar percepatan balok 1 adalah 3,12 m/s2 sedangkan besar percepatan balok 2 adalah 1,56 m/s2. Untuk menentukan besar gaya tegangan tali sistem, maka kita dapat memasukkan nilai a1 ke persamaan (6.3) atau memasukkan nilai a2 ke persamaan (7.3).
T = m1a1 + μkm1g
T = (4)(3,12) + (0,25)(4)(10)
T = 12,48 + 10
T = 22,48 N
Dengan demikian, besar gaya tegangan tali sistem apabila bidang datar kasar adalah 22,48 Newton.
4. Tiga balok bermassa m1, m2 dan m3 dihubungkan dengan tali-tali melalui dua buah katrol. Balok m1 dan m3 dalam keadaan menggantung sedangkan balok m2 berada di atas bidang datar seperti yang diperlihatkan pada gambar berikut ini.

Pada rangkaian di atas, massa balok 1, 2 dan 3 berturut-turut adalah 1 kg, 3 kg dan 6 kg dan percepatan gravitasi bumi di tempat itu adalah 10 m/s2. Kondisi dua katrol adalah licin serta massanya diabaikan. Tentukanlah percepatan ketiga balok, tegangan tali antara balok 1 dan 2 serta tegangan tali antara balok 2 dan 3 apabila Bidang datar kasar dengan koefisien gesek sebesar 0,2.
Penyelesaian
Diketahui:
m1 = 1 kg
m2 = 3 kg
m3 = 6 kg
g = 10 m/s2
μ = 0,2 (bidang datar kasar)
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab
Untuk kondisi datar kasar, maka laju balok akan terhambat oleh gaya gesek sehingga percepatannya menjadi lebih kecil sedangkan gaya tegangan tali antara balok 2 dan balok 3 menjadi lebih besar. Untuk menentukan percepatan ketiga balok, kita gambarkan terlebih dahulu diagram gaya sistem seperti yang diperlihatkan pada gambar di bawah ini.
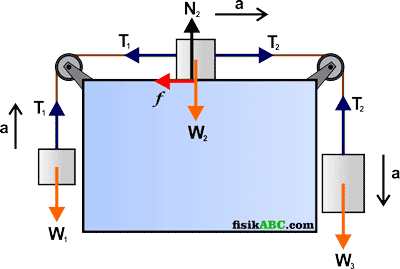
Berdasarkan gambar diagram gaya di atas, maka resultan gaya pada masing-masing balok dapat kita tentukan dengan menggunakan Hukum Newton sebagai berikut.
Tinjau Balok 1
ΣFY = ma
T1 – w1 = m1a
T1 – m1g = m1a
T1 = m1a + m1g ............... Pers. (6.4)
Tinjau Balok 2
ΣFY = ma
N2 – w2 = m2a
Karena tidak ada gerak pada sumbu-Y (arah vertikal) maka a = 0, sehingga
N2 – w2 = 0
N2 = w2
N2 = m2g
ΣFX = ma
T2 – f – T1 = m2a
T2 – μN2 – T1 = m2a
T2 – μm2g – T1 = m2a ............... Pers. (7.4)
Subtitusikan persamaan (6.4) ke persamaan (7.4)
T2 – μm2g – (m1a + m1g) = m2a
T2 = m1a + m2a + m1g + μm2g ............... Pers. (8.4)
Tinjau Balok 3
ΣFY = ma
w3 – T2 = m3a
m3g – T2 = m3a ............... Pers. (9.4)
Subtitusikan persamaan (8.4) ke persamaan (9.4)
m3g – (m1a + m2a + m1g + μm2g) = m3a
m1a + m2a + m3a = m3g – m1g – μm2g
(m1 + m2 + m3)a = (m3 – m1 – μm2)g
a = (m3 – m1 – μm2)g/(m1 + m2 + m3) ............... Pers. (10.4)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (10.4).
a = [6 – 1 – (0,2)(3)]10/(1 + 3 + 6)
a = (5 – 0,6)10/10
a = 4,4 m/s2
Jadi, besar percepatan ketiga balok pada kondisi bidang datar licin adalah 4,4 m/s2. Untuk menentukan besar gaya tegangan tali antara balok 1 dan balok 2, masukkan nilai percepatan ke persamaan (6.4). Sedangkan untuk menentukan gaya tegangan tali antara balok 2 dan balok 3, masukkan nilai percepatan ke persamaan (9.4).
Tegangan Tali antara Balok 1 dengan Balok 2
T1 = m1a + m1g
T1 = (1)(4,4) + (1)(10)
T1 = 4,4 + 10
T1 = 14,4 N
Jadi, besar gaya tegangan tali antara balok 1 dengan balok 2 adalah 14,4 Newton.
Tegangan Tali antara Balok 2 dengan Balok 3
m3g – T2 = m3a
(6)(10) – T2 = (6)(4,4)
60 – T2 = 26,4
T2 = 60 – 26,4
T2 = 33,6 N
Jadi, besar gaya tegangan tali antara balok 2 dengan balok 3 adalah 33,6 Newton.
5. Dua buah balok yaitu balok m1 dan m2 masing-masing bermassa 4 kg dan 6 kg. kedua balok tersebut dihubungkan seutas tali melalui katrol licin dan massanya diabaikan. Balok 1 terletak di bidang miring dengan sudut kemiringan sebesar 30° sedangkan balok 2 dalam posisi menggantung. Tentukanlah besar percepatan dan gaya tegangan tali bila bidang miring licin dan arah gerak ditunjukkan oleh anak panah seperti gambar berikut ini.

Penyelesaian
Diketahui:
m1 = 4 kg
m2 = 6 kg
θ = 30°
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab
Untuk menentukan percepatan dan gaya tegangan tali sistem, langkah pertama adalah menggambarkan diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.

Setelah itu, kita tentukan resultan gaya pada masing-masing balok dengan menggunakan Hukum Newton sebagai berikut.
Tinjau Balok 1
ΣFX = ma
T – w1 sin θ = m1a
T – m1g sin θ = m1a
T = m1a + m1g sin θ …………… Pers. (1.5)
Tinjau Balok 2
ΣFY = ma
w2 – T = m2a
m2g – T = m2a …………… Pers. (2.5)
Subtitusikan persamaan (1.5) ke dalam persamaan (2.5)
m2g – (m1a + m1g sin θ) = m2a
m1a + m2a = m2g – m1g sin θ
(m1 + m2)a = (m2 – m1 sin θ)g
a = (m2 – m1 sin θ)g/(m1 + m2) …………… Pers. (3.5)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (3.5)
a = [6 – (4)(sin 30°)]10/(4 + 6)
a = [6 – (4)(0,5)]10/10
a = 6 – 2
a = 4 m/s2
Jadi besar percepatan kedua balok adalah 4 m/s2. Untuk menentukan besar gaya tegangan tali, kita masukkan nilai percepatan ke persamaan (1.5) sebagai berikut.
T = m1a + m1g sin θ
T = (4)(4) + (4)(10)(sin 30°)
T = 16 + (40)(0,5)
T = 16 + 20
T = 36 N
Dengan demikian, besar gaya tegangan tali yang bekerja pada balok 1 dan 2 adalah 36 Newton.
6. Dua buah balok yaitu balok m1 dan m2 masing-masing bermassa 2 kg dan 4 kg. Kedua balok tersebut dihubungkan seutas tali melalui katrol licin dan massanya diabaikan. Balok m1 dan m2 masing-masing berada di atas bidang miring yang membentuk sudut sebesar 30° dan 60° terhadap arah horizontal. Jika kedua bidang miring licin sempurna, maka tentukanlah besar percepatan dan gaya tegangan tali yang bekerja pada kedua balok tersebut.

Penyelesaian
Diketahui:
m1 = 2 kg
m2 = 4 kg
α = 30°
β = 60°
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab
Pertama kita gambarkan diagram gaya yang bekerja pada sistem. Oleh karena kedua benda berada di atas bidang miring, maka gaya berat keduanya harus kita proyeksikan terhadap sumbu-X dan sumbu-Y bidang miring. Kurang lebih, diagram gaya pada sistem ini ditunjukkan pada gambar di bawah ini.

Karena bidang miring licin dan m2 > m1, maka balok 1 akan bergerak ke atas sedangkan balok 2 akan bergerak turun dengan percepatan yang sama sebesar a. Untuk menentukan percepatan dan tegangan tali, kita tentukan resultan gaya masing-masing balok dengan menggunakan Hukum Newton sebagai berikut.
Tinjau Balok 1
ΣFX = ma
T – w1 sin α = m1a
T – m1g sin α = m1a
T = m1a + m1g sin α ..…….….. Pers. (1.6)
Tinjau Balok 2
ΣFX = ma
w2 sin β – T = m2a
m2g sin β – T = m2a .………... Pers. (2.6)
Subtitusikan persamaan (1.6) ke dalam persamaan (2.6)
m2g sin β – (m1a + m1g sin α) = m2a
m1a + m2a = m2g sin β – m1g sin α
(m1 + m2)a = (m2 sin β – m1 sin α)g
a | = | (m2 sin β – m1 sin α)g | .………... Pers. (3.6) |
m1 + m2 |
Kemudian, masukkan nilai-nilai yang diketahui dalam soal ke persamaan (3.6)
a | = | [(4)(sin 60°) – (2)(sin 30°)]10 |
2 + 4 |
a = [(4)(0,87) – (2)(0,5)]10/6
a = (3,48 – 1)10/6
a = (2,48)10/6
a = 24,8/6
a = 4 m/s2
Jadi besar percepatan kedua balok yang berada di bidang miring licin adalah 4 m/s2. Untuk menentukan besar gaya tegangan tali, kita masukkan nilai percepatan ke persamaan (1.6) sebagai berikut.
T = m1a + m1g sin α
T = (2)(4) + (2)(10)(sin 30°)
T = (8) + (20)(0,5)
T = 8 + 10
T = 18 N
Dengan demikian, besar gaya tegangan tali yang bekerja pada balok 1 dan 2 untuk bidang miring licin adalah 18 Newton.
7. Sebuah benda yang terletak pada bidang miring yang membentuk sudut sebesar 37° terhadap bidang horizontal, dihubungkan dengan benda lain melalui sebuah katrol licin dan massanya diabaikan seperti yang diperlihatkan pada gambar di bawah ini.

Dari gambar di atas diketahui m1 = 2000 g, m2 = 5000 g dan percepatan gravitasi bumi 10 m/s2. Apabila koefisien gesekan kinetis bidang dengan benda 1 adalah 0,2, maka tentukanlah percepatan gerak kedua benda dan besar gaya tegangan tali.
Penyelesaian
Diketahui:
m1 = 2000 g = 2 kg
m2 = 5000 g = 5 kg
θ = 37°
μk = 0,2
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab
Berikut adalah gambar diagram gayanya.

Dengan menggunakan Hukum Newton, resultan gaya pada masing-masing benda adalah sebagai berikut.
Tinjau Benda 1
ΣFY = ma
N – w1 cos θ = m1a
N – m1g cos θ = m1a
Karena tidak terjadi gerak dalam arah vertikal, maka a = 0 sehingga
N – m1g cos θ = 0
N = m1g cos θ
ΣFX = ma
T – w1 sin θ – f = m1a
T – w1 sin θ – μkN = m1a
T – m1g sin θ – μkm1g cos θ = m1a
T = m1a + m1g sin θ + μkm1g cos θ …………… Pers. (4.7)
Tinjau Balok B
ΣFY = ma
w2 – T = m2a
m2g – T = m2a …………… Pers. (5.7)
Subtitusikan persamaan (4.7) ke persamaan (5.7)
m2g – (m1a + m1g sin θ + μkm1g cos θ) = m2a
m1a + m2a = m2g – m1g sin θ – μkm1g cos θ
(m1 + m2)a = (m2 – m1 sin θ – μkm1 cos θ)g
a = (m2 – m1 sin θ – μkm1 cos θ)g/(m1 + m2) …………… Pers. (6.7)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (6.7)
a = [5 – (2)(sin 37°) – (0,2)(2)(cos 37°)]10/(2 + 5)
a = [5 – (2)(0,6) – (0,4)(0,8)]10/7
a = (5 – 1,2 – 0,32)10/7
a = (3,48)10/7
a = 34,8/7
a = 4,97 m/s2 = 5 m/s2
Jadi, besar percepatan gerak kedua benda adalah 5 m/s2. Selanjutnya, besar gaya tegangan tali sistem dapat kita cari dengan cara mensubtitusikan besar percepatan dan nilai yang diketahui dalam soal ke dalam persamaan (5.7) [yang lebih simpel] sebagai berikut.
m2g – T = m2a
T = m2g – m2a
T = m2(g – a)
T = 5(10 – 5)
T = (5)(2)
T = 10 N
Dengan demikian, besar gaya tegangan tali yang bekerja pada sistem tersebut adalah 10 Newton.
8. Tiga buah balok masing-masing bermassa 4 kg, 6 kg dan 10 kg dihubungkan dengan tali-tali melalui dua katrol tetap. Balok m1 terletak pada bidang miring yang membentuk sudut 30° terhadap arah horizontal, balok m2 terletak pada bidang datar sedangkan balok m3 dalam posisi menggantung seperti yang ditunjukkan pada gambar berikut.
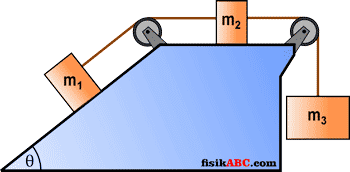
Pada rangkaian seperti pada gambar di atas, kondisi kedua katrol adalah licin serta massa tali dan katrol diabaikan (g = 10 m/s2). Tentukanlah percepatan masing-masing balok, tegangan tali antara balok 1 dengan balok 2 serta tegangan tali antara balok 2 dengan balok 3 jika Bidang miring dan bidang datar kasar dengan koefisien gesek masing-masing sebesar 0,2 dan 0,3.
Penyelesaian
Diketahui:
m1 = 4 kg
m2 = 6 kg
m3 = 10 kg
θ = 30°
μ1 = 0,2 (bidang miring kasar)
μ2 = 0,3 (bidang datar kasar)
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan tali
Jawab
Untuk kondisi bidang miring dan datar kasar, maka laju balok akan terhambat oleh gaya gesek sehingga percepatannya menjadi lebih kecil namun tegangan talinya menjadi lebih besar. Untuk menentukan percepatan ketiga balok, kita gambarkan terlebih dahulu diagram gaya sistem seperti yang diperlihatkan pada gambar berikut.

Berdasarkan gambar diagram gaya di atas, maka resultan gaya pada masing-masing balok dapat kita tentukan dengan menggunakan Hukum Newton sebagai berikut.
Tinjau Balok 1
ΣFY = ma
N1 – w1 cos θ = m1a
N1 – m1g cos θ = m1a
Karena tidak terjadi gerak dalam arah sumbu-Y, maka a = 0 sehingga
N1 – m1g cos θ = 0
N1 = m1g cos θ
ΣFX = ma
T1 – w1 sin θ – f1 = m1a
T1 – m1g sin θ – μ1N1 = m1a
Karena N1 = m1g cos θ maka
T1 – m1g sin θ – μ1m1g cos θ = m1a
T1 = m1a + m1g sin θ + μ1m1g cos θ ………. Pers. (5.8)
Tinjau Balok 2
ΣFY = ma
N2 – w2 = m2a
Karena tidak terjadi gerak dalam arah sumbu-Y, maka a = 0 sehingga
N2 – w2 = 0
N2 – m2g = 0
N2 = m2g
ΣFX = ma
T2 – T1 – f2 = m2a
T2 – T1 – μ2N2 = m2a
Karena N2 = m2g, maka
T2 – T1 – μ2m2g = m2a ………. Pers. (6.8)
Subtitusikan persamaan (5.8) ke persamaan (6.8)
T2 – (m1a + m1g sin θ + μ1m1g cos θ) – μ2m2g = m2a
T2 = m1a + m2a + m1g sin θ + μ1m1g cos θ + μ2m2g ………. Pers. (7.8)
Tinjau Balok 3
ΣFY = ma
w3 – T2 = m3a
m3g – T2 = m3a ………. Pers. (8.8)
Subtitusikan persamaan (7.8) ke dalam persamaan (8.8)
m3g – (m1a + m2a + m1g sin θ + μ1m1g cos θ + μ2m2g) = m3a
m1a + m2a + m3a = m3g – m1g sin θ – μ1m1g cos θ – μ2m2g
(m1 + m2 + m3)a = (m3 – m1 sin θ – μ1m1 cos θ – μ2m2)g
a | = | (m3 – m1 sin θ – μ1m1 cos θ – μ2m2)g | ………. Pers. (9.8) |
m1 + m2 + m3 |
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (6.8)
a | = | [10 – (4)(sin 30°) – (0,2)(4)(cos 30°) – (0,3)(6)]10 |
4 + 6 + 10 |
a | = | [10 – (4)(0,5) – (0,8)(0,87) – (1,8)]10 |
20 |
a | = | 10 – 2 – 0,7 – 1,8 |
2 |
a = 5,5/2
a = 2,75 m/s2
Jadi, besar percepatan ketiga balok untuk kondisi bidang kasar adalah 2,75 m/s2. Untuk menentukan besar gaya tegangan tali antara balok 1 dan balok 2, masukkan nilai percepatan ke persamaan (5.8). Sedangkan untuk menentukan tegangan tali antara balok 2 dan balok 3, masukkan nilai percepatan ke persamaan (8.8).
Tegangan Tali antara Balok 1 dengan Balok 2
T1 = m1a + m1g sin θ + μ1m1g cos θ
T1 = (4)(2,74) + (4)(10)(sin 30°) + (0,2)(4)(10)(cos 30°)
T1 = 10,96 + (40)(0,5) + (8)(0,87)
T1 = 10,96 + 20 + 6,96
T1 = 38 N
Jadi, besar gaya tegangan tali antara balok 1 dengan balok 2 adalah 38 Newton.
Tegangan Tali antara Balok 2 dengan Balok 3
m3g – T2 = m3a
(10)(10) – T2 = (10)(2,75)
100 – T2 = 27,5
T2 = 100 – 27,5
T2 = 72,5 N
Jadi, besar gaya tegangan tali antara balok 2 dengan balok 3 adalah 72,5 Newton.