Contoh Soal Gaya Normal pada Bidang Miring + Jawabannya Lengkap dan Mudah
Daftar Materi Fisika
Gaya Normal adalah gaya yang bekerja pada bidang yang bersentuhan antara dua permukaan benda, yang arahnya selalu tegak lurus dengan bidang sentuh. Lambang gaya normal adalah N dan satuan Sistem Internasionalnya adalah kgm/s2 atau Newton.
Nah pada kesempatan kali ini kita akan membahas mengenai bebebrapa contoh soal dan penyelesaian tentang gaya normal pada bidang miring, baik itu bidang miring licin maupun bidang miring kasar. Oleh karena itu silahkan kalian simak baik-baik contoh soal berikut ini.
1. Sebuah balok bermassa 5 kg. jika g = 10 m/s2 maka tentukan gaya normal yang bekerja pada balok jika diam di atas bidang miring yang membentuk sudut 300 terhadap horisontal.
Jawab

Perhatikan gambar di atas. gaya-gaya pada balok dapat dilihat pada gambar tersebut. Balok dalam keadaan diam pada arah tegak lurus bidang berarti berlaku persamaan berikut.
ΣFY = 0
N – w cos α = 0
N – w cos 30o = 0
N – 50 × ½ √3 = 0
N = 25 √3 N
2. Balok bermassa 2 kg berada dalam keadaan diam di atas sebuah bidang dengan sudut kemiringan sebesar 30o. Apabila besar percepatan gravitasi bumi adalah 10 m/s2, hitunglah gaya normal yang dialami balok tersebut!
Pembahasan:
Diketahui:
m = 2 kg
θ = 30o
g = 10 m/s2
Ditanyakan: gaya normal (N)
Jawab:
Garis-garis gaya yang bekerja pada balok tersebut ditunjukan seperti pada diagram di bawah ini.
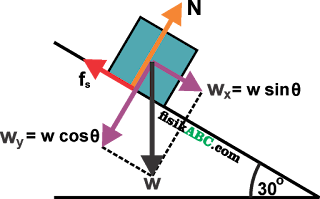
Seperti yang telah diketahui dalam soal, balok berada dalam keadaan diam itu artinya tidak terjadi gerakan baik dalam arah sumbu-Y maupun sumbu-X. Karena kita akan menghitung besarnya gaya normal yang dialami balok, maka kita hanya fokus pada gaya-gaya yang bekerja pada sumbu-Y saja.
ΣFY = 0
N – wy = 0
N = wy
N = w cos θ
N = mg cos θ
N = (2)(10)(cos 30o)
N = 20 × ½√3
N = 10√3 N
3. Balok A dan balok B terletak di atas permukaan bidang miring licin dengan sudut kemiringan 37°. Massa balok A 40 kg dan massa balok B 20 kg. Kemudian balok A didorong dengan gaya F sebesar 480 N seperti yang diperlihatkan pada gambar di bawah ini. Tentukan besar gaya normal, percepatan gerak kedua balok dan juga gaya kontak antara balok A dan balok B.

Jawab
Diketahui:
mA = 40 kg
mB = 20 kg
F = 480 N
θ = 37°
g = 10 m/s2
Ditanyakan: Gaya normal, percepatan dan gaya kontak.
Langkah pertama adalah menggambarkan diagram gaya yang bekerja pada masing-masing balok secara terpisah untuk mempermudah membedakan gaya-gaya mana yang bekerja pada kedua balok. Perhatikan gambar di bawah ini.

FAB adalah gaya aksi yang diberikan balok A kepada balok B, sedangkan FBA adalah gaya reaksi yang diberikan balok B kepada balok A. Kedua gaya tersebut merupakan gaya kontak yang besarnya sama. Lalu untuk menentukan besar percepatan kedua balok dan juga gaya kontak, kita tinjau persamaan gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.
∎ Tinjau Balok A
Resultan gaya pada sumbu-Y
ΣFY = ma
ΣFY = 0
NA – WA cos θ = 0
NA = WA cos θ
NA = mA g cos θ
NA = (40)(10)(cos 37°)
NA = (400)(0,8)
NA = 320 N
Dengan demikian, gaya normal balok A sebesar 320 Newton.
Resultan gaya pada sumbu-X:
ΣFX = ma
F – wA sin θ – FBA = mAa
F – mAg sin θ – FBA = mAa ............... Pers. (1.3)
∎ Tinjau Balok B
Resultan gaya pada sumbu-Y
ΣFY = ma
ΣFY = 0
NB – WB cos θ = 0
NB = WB cos θ
NB = mB g cos θ
NB = (20)(10)(cos 37°)
NB = (200)(0,8)
NB = 160 N
Dengan demikian, gaya normal balok A sebesar 160 Newton.
Resultan gaya pada sumbu-X
ΣFX = ma
FAB – wA sin θ = mBa
FAB – mBg sin θ = mBa
FAB = mBa + mBg sin θ ............... Pers. (2.3)
Karena FAB = FBA, maka kita dapat mensubtitusikan persamaan (2.3) ke dalam persamaan (1.3) sebagai berikut.
F – mAg sin θ – (mBa + mBg sin θ) = mAa
F – mAg sin θ – mBa – mBg sin θ = mAa
F – mAg sin θ – mBg sin θ = mAa + mBa
F – g sin θ(mA + mB) = (mA + mB)a
a = [F – g sin θ(mA + mB)]/(mA + mB)
a = [F/(mA + mB)] – g sin θ ............... Pers. (3.3)
Dengan mensubtitusikan nilai-nilai yang diketahui dalam soal ke dalam persamaan (3.3), maka kita peroleh besar percepatan kedua balok sebagai berikut.
a = [480/(40 + 20)] – (10) sin 37°
a = (480/60) – (10)(0,6)
a = 8 – 6
a = 2 m/s2
Jadi, besar percepatan kedua balok adalah 2 m/s2. Untuk menentukan gaya kontak antara balok A dan B, kita subtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (2.3) sebagai berikut.
FAB = mBa + mBg sin θ
FAB = (20)(2) + (20)(10)(sin sin 37°)
FAB = 40 + (200)(0,6)
FAB = 40 + 120
FAB = 160 N
Dengan demikian, besar gaya kontak antara balok A dan balok B adalah 160 N.
4. Sebuah balok yang massanya 6 kg meluncur ke bawah pada sebuah papan licin yang dimiringkan 30ᵒ dari lantai. Jika jarak lantai dengan balok 10 m dan besarnya percepatan gravitasi di tempat itu adalah 10 ms-2, maka tentukan gaya normal, percepatan dan waktu yang diperlukan balok untuk sampai di lantai.
Jawab
Diketahui:
m = 6 kg
s = 10 m
θ = 30ᵒ
g = 10 m/s
Ditanyakan: Gaya normal, percepatan dan waktu.
Langkah pertama untuk menyelesaikan soal yang berhubungan dengan dinamika gerak adalah menggambarkan skema ilustrasi soal beserta diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.
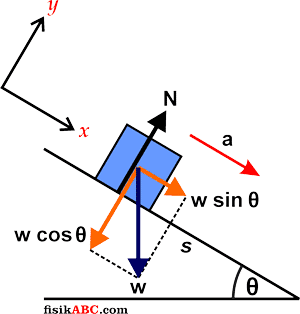
Menurut Hukum II Newton, resultan gaya yang bekerja pada benda dalam arah sumbu-X dan sumbu-Y adalah sebagai berikut.
Resultan gaya pada sumbu-Y:
ΣFY = ma
ΣFY = 0
N – W cos θ = 0
N = W cos θ
N = m g cos θ
N = (6)(10)(cos 30°)
N = (60)(1/2√3)
N = 30√3 N
Dengan demikian, gaya normal balok sebesar 30√3 Newton.
Resultan gaya pada sumbu-X:
ΣFX = ma
w sin θ = ma
mg sin θ = ma
a = g sin θ …………… Pers. (1.4)
■ Menentukan percepatan
Untuk menentukan besar percepatan balok, subtitusikan nilai-nilai yang diketahui dalam soal ke persamaan (1.4) sebagai berikut.
a = g sin θ
a = (10)(sin 30ᵒ)
a = (10)(0,5)
a = 5 m/s2
jadi, balok tersebut meluncur ke bawah dengan percepatan sebesar 5 m/s2.
■ Menentukan waktu untuk sampai di lantai
Untuk menentukan waktu yang diperlukan balok untuk mencapai lantai, kita gunakan rumus jarak pada gerak lurus berubah beraturan atau GLBB. (Kenapa GLBB bukan GLB?).
s = v0t + ½ at2
karena tidak ada keterangan mengenai kecepatan awal, maka v0 = 0 sehingga
s = ½ at2
t2 = 2s/a
t = √(2s/a) …………… Pers. (2.4)
Subtitusikan besar percepatan dan nilai yang diketahui dalam soal ke persamaan (2.4)
t = √[(2)(10)/5]
t = √(20/5)
t = √4
t = 2 m/s2
Dengan demikian, waktu yang diperlukan balok untuk sampai ke lantai adalah 2 detik.
5. Balok bermassa 20 kg berada di atas bidang miring licin dengan sudut kemiringan 30o. Jika Ucok ingin mendorong ke atas sehingga kecepatannya tetap maka berapakah gaya yang harus diberikan oleh Ucok dan besarnya gaya normal balok tersebut?
Penyelesaian:
m = 20 kg
g = 10 m/s2
w = mg = 20 × 10 = 200 N
α = 30o
Gaya dorong Ucok F harus dapat mengimbangi proyeksi gaya berat. Lihat gambar di bawah ini. Balok bergerak ke atas dengan kecepatan tetap berarti masih berlaku hukum I Newton sehingga memenuhi persamaan berikut.
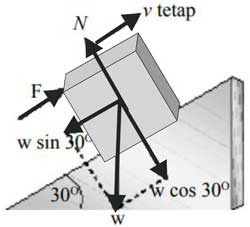
ΣFX = 0
F – w sin 30o = 0
F – (200)(1/2) = 0
F – 100 = 0
F = 100 N
Jadi, gaya yang harus diberikan pada balok agar balok bergerak dengan kecepatan tetap adalah sebesar 100 N.
Sementara itu, gaya normal yang dialami balok tersebut adalah sebagai berikut.
ΣFY = 0
N – W cos θ = 0
N = W cos θ
N = m g cos θ
N = (20)(10)(cos 30°)
N = (200)(1/2√3)
N = 100√3 N
Dengan demikian, gaya normal balok sebesar 100√3 Newton.
6. Sebuah peti kayu bermassa 60 kg didorong oleh seseorang dengan gaya 800 N ke atas sebuah truk menggunakan papan yang disandarkan membentuk bidang miring. Ketinggian bak truk tempat papan bersandar adalah 2 m dan panjang papan yang digunakan adalah 2,5 m. Jika peti bergerak ke atas dengan percepatan 2 m/s2 dan g = 10 m/s2 maka tentukan gaya normal peti kayu dan koefisien gesek kinetis antara peti kayu dengan papan.
Jawab
Diketahui:
m = 60 kg
F = 800 N
a = 2 m/s2
tinggi bak (y) = 2 m
Panjang papan (r) = 2,5 m
g = 10 m/s
Ditanyakan: Gaya normal dan koefisien gesek kinetik
Ketika peti berada di atas papan, diagram gaya-gaya yang bekerja dapat kalian lihat pada gambar berikut ini.
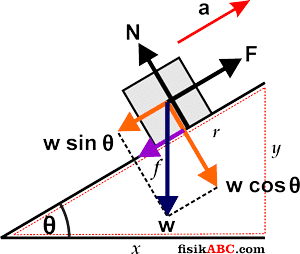
Karena sudut kemiringan bidang tidak diketahui, maka kita perlu mengetahui panjang sisi-sisi bidang miring. Dari soal, panjang sisi yang belum diketahui adalah sisi horizontal atau bisa kita misalkan sebagai x. Dengan menggunakan Teorema Phytagoras, maka panjang x adalah sebagai berikut.
x2 = r2 – y2
x2 = (2,5)2 – (2)2
x2 = 6,25 – 4
x2 = 2,25
x = √2,25 = 1,5 m
langkah selanjutnya adalah kita tentukan resultan gaya yang bekerja pada sumbu-X dan sumbu-Y dengan menggunakan Hukum Newton sebagai berikut.
Resultan Gaya pada Sumbu-Y
ΣFY = ma
N – w cos θ = ma
Karena tidak terjadi gerak pada arah vertikal, maka a = 0 sehingga
N – w cos θ = 0
N – mg cos θ = 0
N = mg cos θ
N = mg (x/r)
N = (60)(10)(1,5/2,5)
N = (600(3/5)
N = 360
Dengan demikian, gaya normal yang dialami peti kayu adalah sebesar 360 N.
Resultan Gaya pada Sumbu-X
ΣFX = ma
F – w sin θ – f = ma
F – mg sin θ – μkN = ma
F – mg sin θ – μkmg cos θ = ma
μkmg cos θ = F – mg sin θ – ma
μkmg(x/r) = F – mg(y/r) – ma
kemudian kita masukkan nilai-nilai yang diketahui dari soal ke persamaan di atas.
μk(60)(10)(1,5/2,5) = 800 – (60)(10)(2/2,5) – (60)(2)
360μk = 800 – 480 – 120
360μk = 200
μk = 200/360
μk = 0,56
Jadi, besar koefisien gesek kinetis antara peti kayu dengan papan adalah 0,56.