Contoh Soal Katrol Gabungan dan Jawabannya Lengkap
https://www.fisikabc.com/2018/09/contoh-soal-katrol-gabungan.html?m=1
Daftar Materi Fisika
Advertisement
Baca Juga:
Pada kesempatan kali ini, penulis akan memberikan beberapa contoh soal tentang katrol gabungan (sistem katrol) beserta pembahasannya. Katrol gabungan yang dimaksud dalam konteks ini adalah kombinasi antara katrol tetap dan katrol bebas.
Apa itu katrol tetap?
Seperti namanya yang disebut katrol “tetap” adalah katrol yang tetap pada tempatnya, tidak berpindah tempat dalam penggunaannya. Contoh paling mudah sobat temui adalah kerekan sumur.
Apa itu katrol bebas?
Katrol bergerak adalah katrol dengan salah satu ujung tali terikat pada tempat tetap dan ujung yang lain ditarik ke atas oleh sebuah gaya. Benda yag akan diangkat digantungkan pada poros katrol sehingga besar beban totoal adalah berat katrol ditambah dengan berat benda.
Nah, sebelum masuk ke pembahasan contoh soal, kita perlu mempelajari konsep tentang Hukum Newton dan perjanjian tanda untuk gaya yang bekerja pada sistem katrol berikut ini.
Konsep Hukum Newton
Hukum I Newton
|
Hukum II Newton
|
Hukum III Newton
|
ΣF = 0
|
ΣF = ma
|
Faksi = −Freaksi
|
Keadaan benda:
■ diam (v = 0 m/s)
|
Keadaan benda:
|
Sifat gaya aksi reaksi:
■ sama besar
■ berlawanan arah
■ terjadi pada 2 objek berbeda
|
Perjanjian Tanda
Gaya
|
Syarat
|
Gaya berharga positif
|
Jika searah dengan arah gerak benda (bisa dilihat dari arah percepatan gerak benda).
|
Gaya berharga negatif
|
Jika berlawanan dengan arah gerak benda.
|
Baiklah, jika kalian sudah paham mengenai konsep Hukum Newton dan perjanjian tanda untuk gaya-gaya yang bekerja pada sistem katrol, kini saatnya kita bahas contoh soal katrol gabungan. Simak baik-baik uraian berikut ini.
1. Tiga balok yaitu balok m1, m2 dan m3 dihubungkan dengan seutas tali melalui sistem katrol gabungan. Balok m1 dan m2 dihubungkan pada katrol tetap sedangkan balok m3 dihubungkan pada katrol bebas bergerak seperti yang diperlihatkan pada gambar berikut ini.
1. Tiga balok yaitu balok m1, m2 dan m3 dihubungkan dengan seutas tali melalui sistem katrol gabungan. Balok m1 dan m2 dihubungkan pada katrol tetap sedangkan balok m3 dihubungkan pada katrol bebas bergerak seperti yang diperlihatkan pada gambar berikut ini.
Dari gambar di atas,
diketahui massa balok 1, 2 dan 3 berturut-turut adalah 2 kg, 4 kg dan 8
kg. Percepatan gravitasi bumi di tempat itu sebesar 10 m/s2.
Apabila katrol licin serta massa tali dan katrol diabaikan, maka
tentukanlah gaya tegangan tali sistem dan percepatan masing-masing
balok!
Penyelesaian
Diketahui:
m1 = 2 kg
m2 = 4 kg
m3 = 8 kg
g = 10 m/s2
Ditanyakan: Gaya tegangan tali dan percepatan
Jawab
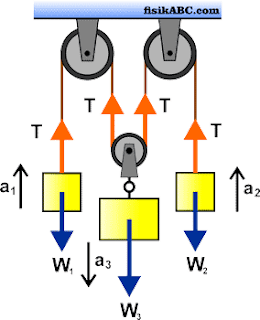
Dari data soal diketahui bahwa m3 > m1 + m2 sehingga balok 1 akan bergerak naik dengan percepatan a1, balok 2 akan bergerak naik dengan percepatan a2 sedangkan balok 3 akan bergerak turun dengan percepatan a3. Diagram gaya yang bekerja pada sistem ini diperlihatkan pada gambar di bawah ini.
Untuk menentukan besar gaya tegangan tali serta percepatan ketiga balok, kita uraikan dahulu persamaan gerak (resultan gaya) dengan meninjau masing-masing balok secara terpisah menggunakan Hukum II Newton sebagai berikut.
Tinjau Balok 1
ΣFY = ma
T – w1 = m1a1
T – m1g = m1a1
a1
|
=
|
T – m1g
|
………. Pers. (1a)
|
m1
|
Tinjau Balok 2
ΣFY = ma
T – w2 = m2a2
T – m2g = m2a2
a2
|
=
|
T – m2g
|
………. Pers. (2a)
|
m2
|
Tinjau Balok 3
ΣFY = ma
w3 – 2T = m3a3
m3g – 2T = m3a3
a3
|
=
|
m3g – 2T
|
………. Pers. (3a)
|
m3
|
Untuk tiga benda yang dihubungkan pada katrol tetap dan katrol bebas, maka besar percepatan
benda pada katrol bebas adalah setengah kali jumlah percepatan dua
benda pada katrol tetap. Secara matematis, hubungan percepatan balok 1, 2
dan 3 dituliskan dalam rumus berikut ini.
a3 = ½ (a1 + a2) ………. Pers. (4b)
Apabila kita subtitusikan persamaan (1b), (2b) dan (3b) ke dalam persamaan (4b) maka akan kita peroleh:
m3g – 2T
|
=
|
1
|
(
|
T – m1g
|
+
|
T – m2g
|
)
| |
m3
|
2
|
m1
|
m2
|
Kalikan kedua ruas dengan angka 2
2m3g – 4T
|
=
|
T – m1g
|
+
|
T – m2g
| |
m3
|
m1
|
m2
|
Kemudian sederhanakan ruas kanan
2m3g – 4T
|
=
|
m2T – m1m2g + m1T – m1m2g
| |
m3
|
m1m2
|
2m3g – 4T
|
=
|
m2T + m1T – 2m1m2g
| |
m3
|
m1m2
|
Dengan menggunakan asas perkalian silang, maka persamaan di atas menjadi
2m1m2m3g – 4m1m2T = m2m3T + m1m3T – 2m1m2 m3g
4m1m2T + m1m3T + m2m3T = 2m1m2m3g + 2m1m2 m3g
(4m1m2 + m1m3 + m2m3)T = 4m1m2m3g
T = 4m1m2m3g/(4m1m2 + m1m3 + m2m3) ………. Pers. (5b)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (5b)
T = (4)(2)(4)(8)(10)/[(4)(2)(4) + (2)(8) + (4)(8)]
T = 2560/(32 + 16 + 32)
T = 2560/80
T = 32 N
Jadi, besarnya gaya tegangan tali sistem
adalah 32 Newton. Untuk menentukan percepatan masing-masing balok, kita
dapat memasukkan nilai tegangan tali yang sudah kita peroleh ke dalam
persamaan (1b), (2b) dan (3b).
Percepatan Balok 1
a1
|
=
|
T – m1g
|
m1
|
a1 = [32 – (2)(10)]/2
a1 = (32 – 20)/2
a1 = 12/2
a1 = 6 m/s2
Jadi, besar percepatan balok 1 adalah 6 m/s2
Percepatan Balok 2
a2
|
=
|
T – m2g
|
m2
|
a2 = [32 – (4)(10)]/4
a2 = (32 – 40)/4
a2 = −8/4
a2 = −2 m/s2
Jadi, balok 2 mengalami perlambatan sebesar −2 m/s2
Percepatan Balok 3
a3
|
=
|
m3g – 2T
|
m3
|
a3 = [(8)(10) – (2)(32)]/8
a3 = (80 – 64)/8
a3 = 16/8
a3 = 2 m/s2
Jadi, besar percepatan balok 1 adalah 2 m/s2
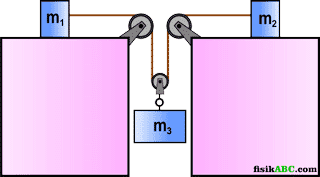
2. Tiga balok yaitu balok m1, m2 dan m3 dihubungkan dengan seutas tali melalui sistem katrol gabungan. Balok m1 dan m2 dihubungkan pada katrol tetap dan terletak pada bidang datar sedangkan balok m3 menggantung pada katrol bebas bergerak seperti yang diperlihatkan pada gambar berikut ini.
Dari gambar di atas,
diketahui massa balok 1, 2 dan 3 berturut-turut adalah 2 kg, 3 kg dan 5
kg. Percepatan gravitasi bumi di tempat itu sebesar 10 m/s2.
Keadaan tiga katrol tersebut adalah licin sempurna serta massa tali dan
katrol diabaikan. Tentukanlah gaya tegangan tali sistem dan percepatan
masing-masing balok apabila bidang datar licin!
Penyelesaian
Diketahui:
m1 = 2 kg
m2 = 3 kg
m3 = 5 kg
g = 10 m/s2
Ditanyakan: Gaya tegangan tali dan percepatan
Jawab
Untuk kondisi bidang datar licin, maka sistem akan bergerak di mana balok 1 akan bergerak ke kanan dengan percepatan a1, balok 2 akan bergerak ke kiri dengan percepatan a2 dan balok 3 akan bergerak ke bawah dengan percepatan a3. Diagram gaya yang bekerja pada sistem ini diperlihatkan pada gambar berikut ini.
Besar gaya tegangan tali
dan percepatan ketiga balok dapat kita tentukan dengan cara menguraikan
terlebih dahulu resultan gaya masing-masing balok menggunakan Hukum II Newton sebagai berikut.
Tinjau Balok 1
ΣFX = ma
T = m1a1
a1
|
=
|
T
|
………. Pers. (1b)
|
m1
|
Tinjau Balok 2
ΣFX = ma
T = m2a2
a2
|
=
|
T
|
………. Pers. (2b)
|
m2
|
Tinjau Balok 2
ΣFY = ma
w3 – 2T = m3a3
m3g – 2T = m3a3
a3
|
=
|
m3g – 2T
|
………. Pers. (3b)
|
m3
|
Untuk tiga benda yang dihubungkan pada katrol tetap dan katrol bebas, maka besar percepatan
benda pada katrol bebas adalah setengah kali jumlah percepatan dua
benda pada katrol tetap. Secara matematis, hubungan percepatan balok 1b, 2b
dan 3b dituliskan dalam rumus berikut ini.
a3 = ½ (a1 + a2) ………. Pers. (4b)
Apabila kita subtitusikan persamaan (1b), (2b) dan (3b) ke dalam persamaan (4b) maka akan kita peroleh:
m3g – 2T
|
=
|
1
|
(
|
T
|
+
|
T
|
)
|
m3
|
2
|
m1
|
m2
|
Kita kalikan kedua ruas dengan angka 2
2m3g – 4T
|
=
|
T
|
+
|
T
|
m3
|
m1
|
m2
|
Kita samakan penyebut pada ruas kanan
2m3g – 4T
|
=
|
m2T + m1T
|
m3
|
m1m2
|
Dengan menggunakan prinsip perkalian silang, maka persamaan diatas menjadi
2m1m2m3g – 4m1m2T = m2m3T + m1m3T
4m1m2T + m1m3T + m2m3T = 2m1m2m3g
(4m1m2 + m1m3 + m2m3)T = 2m1m2m3g
T = 2m1m2m3g/(4m1m2 + m1m3 + m2m3) ………. Pers. (5b)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (5b)
T = (2)(2)(3)(5)(10)/[(4)(2)(3) + (2)(5) + (3)(5)]
T = 600/(24 + 10 + 15)
T = 600/49
T = 12 N
Jadi, besarnya gaya tegangan tali
pada sistem katrol tersebut adalah 12 Newton. Untuk menentukan
percepatan masing-masing balok, kita dapat memasukkan nilai tegangan
tali yang sudah kita peroleh ke dalam persamaan (1b), (2b) dan (3b).
Percepatan Balok 1
a1
|
=
|
T
|
m1
|
a1 = 12/2
a1 = 6 m/s2
Jadi, besar percepatan balok 1 adalah 6 m/s2
Percepatan Balok 2
a2
|
=
|
T
|
m2
|
a2 = 12/3
a2 = 4 m/s2
Jadi, besar percepatan balok 2 adalah 4 m/s2
Percepatan Balok 3
a3
|
=
|
m3g – 2T
|
m3
|
a3 = [(5)(10) – (2)(12)]/5
a3 = (50 – 24)/5
a3 = 26/5
a3 = 5 m/s2
Jadi, besar percepatan balok 1 adalah 5 m/s2


Min mau nanya dong. Gambar katrolnya pakai aplikasi apa yah? Thank you.
ReplyDelete