10+ Contoh Soal Gaya Berat, Normal, Gesek, Tegangan Tali, Sentripetal, Kontak dan Pembahasan Bagian 2

Daftar Materi Fisika

• 1. Besaran Fisika
• 2. Vektor dan Resultan
• 3. Mekanika (Kinematika dan Dinamika)
• 4. Fisika Optik
• 5. Suhu dan Kalor

Advertisement

Baca Juga:

5. Contoh Soal Gaya Sentripetal

1. Sebuah bola bermassa 2 kg diikatkan di ujung seutas tali dan kemudian diputar dalam bidang horizontal dengan kelajuan tetap 5 m/s seperti yang tampak pada gambar di bawah ini. Apabila jari-jari lingkaran 1 m, tentukan besar gaya tegangan talinya.

Jawab:

Diketahui: m = 2 kg, v = 5 m/s dan R = 1 m. Dengan persamaan (2) maka kita peroleh hasil sebagai berikut.

ΣFs = mv2/R

Gaya-gaya yang bekerja dalam arah radial hanya gaya tegangan tali T saja sehingga

T = mv2/R

T = (2 kg)(5 m/s)2/(1 m)

T = 50 N

Dengan demikian, besar gaya tegangan talinya adalah 50 N.

2. Sebuah mobil bermassa 1.000 kg melintasi suatu jembatan yang melengkung. Jari-jari kelengkungan jembatan 20 m denga pusat berada di bawah jembatan. Tentukan besar gaya yang diberikan mobil pada jembatan saat mobil berada di puncak jembatan jika kelajuannya 36 km/jam.

Jawab:

Diketahui: m = 1000 kg, R = 20 m dan v = 36 km/jam = 10 m/s (gunakan metode konversi satuan). Gaya yang diberikan mobil pada jembatan sama dengan gaya yang diberikan jembatan pada mobil, yakni gaya normal seperti yang diperlihatkan pada gambar di atas.

Selain gaya normal, pada mobil bekerja gaya berat. Kedua gaya ini merupakan gaya sentripetal karena bekerja dalam arah radial (berhimpit dengan diameter lingkaran) dengan arah yang saling berlawanan. Dengan menggunakan persamaan (2), kita peroleh:

ΣFs = mv2/R

w – N = mv2/R

mg – N = mv2/R

N = mg – (mv2/R)

N = (1000 kg)(10 m/s2) – {(1000 kg)(10 m/s)2/(20 m)}

N = 10.000 N – 5.000 N

N = 5.000 N

Dengan demikian, besar gaya yang diberikan mobil pada jembatan pada saat mobil berada di puncak jembatan adalah 5.000 N.

6. Contoh Soal Gaya Kontak

1. Dua balok (m1 dan m2) yang bersentuhan mula-mula diam di atas lantai licin seperti yang ditunjukkan pada gambar di bawah ini. Jika m1 = 70 kg, m2 = 30 kg dan pada balok pertama dikerjakan gaya sebesar 200 N, maka tentukanlah percepatan masing-masing balok dan gaya kontak antarbalok tersebut.

Jawab

Diketahui:

m1 = 70 kg

m2 = 30 kg

F = 200 N

Ditanyakan: Percepatan dan gaya kontak.

Pertama, kita gambarkan terlebih dahulu diagram gaya yang bekerja pada kedua benda tersebut. Dan perlu kalian ketahui bahwa keadaan benda 1 dan 2 saling bersentuhan sehingga akan timbul gaya kontak atau gaya aksi reaksi berdasarkan Hukum III Newton. Supaya lebih jelas, perhatikan gambar berikut ini.

F12 adalah gaya aksi yang diberikan balok 1 kepada balok 2 (bekerja pada balok 2). Sedangkan F21 adalah gaya reaksi yang diberikan balok 2 kepada balok 1 (bekerja pada balok 1). Kedua gaya ini memiliki besar yang sama. Untuk menentukan besar percepatan kedua balok dan juga gaya kontak kita tinjau persamaan gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.

∎ Tinjau Balok 1

Karena lantai licin maka tidak ada gaya gesek yang bekerja, sehingga resultan gaya pada sumbu-Y tidak perlu diuraikan.

ΣFX = ma

F – F21 = m1a ............... Pers. (1)

∎ Tinjau Balok 2

ΣFX = ma

F12 = m2a ............... Pers. (2)

Karena F12 = F21, maka kita dapat mensubtitusikan persamaan (2) ke dalam persamaan (1) sebagai berikut.

F – m2a = m1a

F = m1a + m2a

F = (m1 + m2)a

a = F/(m1 + m2) ............... Pers. (3)

Dengan memasukkan nilai yang diketahui dalam soal ke dalam persamaan (3), maka kita peroleh besar percepatan kedua balok sebagai berikut.

a = 200/(70 + 30)

a = 200/100

a = 2 m/s2

Jadi, besar percepatan kedua balok adalah 2 m/s2. Untuk menentukan gaya kontak antara balok 1 dan 2, kita subtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (2) sebagai berikut.

F12 = m2a

F12 = (30)(2)

F12 = 60 N

Dengan demikian, besar gaya kontak antarbalok adalah 60 N.

2. Benda bermassa m1 = 20 kg diletakkan di atas benda yang bermassa m2 = 50 kg. Kemudian kedua benda tersebut didorong vertikal ke atas dengan gaya sebesar 210 N. Jika besar percepatan gravitasi g = 10 m/s2 maka tentukan besar percepatan kedua benda dan juga gaya aksi-reaksi (gaya kontak) antara benda m1 dan m2.

Jawab

Diketahui:

m1 = 20 kg

m2 = 50 kg

F = 210 N

g = 10 m/s2

Ditanyakan: Percepatan dan gaya kontak

Langkah pertama adalah menggambarkan keadaan objek seperti yang dideskripsikan dalam soal beserta diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.

Konsep penyelesaian soal 2 ini sama dengan penyelesaian pada soal 1 hanya saja untuk soal 2, resultan gaya yang perlu kita uraikan adalah resultan gaya pada sumbu-Y. Dalam menentuka besar percepatan dan gaya kontak, kita gunakan Hukum II Newton pada masing-masing benda.

∎ Tinjau Benda 1

ΣFY = ma

F – w1 – F21 = m1a

F – m1g – F21 = m1a ............... Pers. (4)

∎ Tinjau Benda 2

ΣFY = ma

F12 – w2 = m2a

F12 = m2a + w2

F12 = m2a + m2g ............... Pers. (5)

F12 dan F21 merupakan pasangan gaya aksi-reaksi sehingga besarnya sama. Dengan demikian kita dapat mensubtitusikan persamaan (5) ke dalam persamaan (4) sebagai berikut.

F – m1g – (m2a + m2g) = m1a

F – m1g – m2a – m2g = m1a

F – m1g – m2g = m1a + m2a

F – g(m1 + m2) = (m1 + m2)a

a = [F – g(m1 + m2)]/(m1 + m2)

a = [F/(m1 + m2)] – g ............... Pers. (6)

kemudian kita subtitusikan nilai-nilai yang diketahui dalam soal ke persamaan (6) untuk menentukan besar percepatan.

a = [210/(20 + 50)] – 10

a = (210/70) – 10

a = 3 – 10

a = –7 m/s2

Jadi besar percepatan kedua benda tersebut adalah –7 m/s2. Tanda minus menyatakan bahwa benda melakukan gerak vertikal ke atas (GVA) sehingga arah percepatan (a) berlawanan arah dengan percepatan gravitasi bumi (g). Besar gaya kontak dapat kita hitung dengan memasukkan nilai percepatan ke persamaan (5).

F12 = m2a + m2g

F12 = (50)(–7) + (50)(10)

F12 = –350 + 500

F12 = 150 N

Jadi besar gaya aksi-reaksi atau gaya kontak antara benda m1dan m2 adalah 150 N.

3. Balok A dan balok B terletak di atas permukaan bidang miring licin dengan sudut kemiringan 37°. Massa balok A 40 kg dan massa balok B 20 kg. Kemudian balok A didorong dengan gaya F sebesar 480 N seperti yang diperlihatkan pada gambar di bawah ini. Tentukan besar percepatan gerak kedua balok dan juga gaya kontak antara balok A dan balok B.

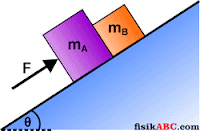
Jawab

Diketahui:

mA = 40 kg

mB = 20 kg

F = 480 N

θ = 37°

g = 10 m/s2

Ditanyakan: Percepatan dan gaya kontak.

Langkah pertama adalah menggambarkan diagram gaya yang bekerja pada masing-masing balok secara terpisah untuk mempermudah membedakan gaya-gaya mana yang bekerja pada kedua balok. Perhatikan gambar di bawah ini.

FAB adalah gaya aksi yang diberikan balok A kepada balok B, sedangkan FBA adalah gaya reaksi yang diberikan balok B kepada balok A. Kedua gaya tersebut merupakan gaya kontak yang besarnya sama. Lalu untuk menentukan besar percepatan kedua balok dan juga gaya kontak, kita tinjau persamaan gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.

∎ Tinjau Balok A

Karena bidang miring licin maka tidak ada gaya gesek yang bekerja, sehingga resultan gaya pada sumbu-Y tidak perlu diuraikan.

ΣFX = ma

F – wA sin θ – FBA = mAa

F – mAg sin θ – FBA = mAa ............... Pers. (1)

∎ Tinjau Balok B

ΣFX = ma

FAB – wA sin θ = mBa

FAB – mBg sin θ = mBa

FAB = mBa + mBg sin θ ............... Pers. (2)

Karena FAB = FBA, maka kita dapat mensubtitusikan persamaan (2) ke dalam persamaan (1) sebagai berikut.

F – mAg sin θ – (mBa + mBg sin θ) = mAa

F – mAg sin θ – mBa – mBg sin θ = mAa

F – mAg sin θ – mBg sin θ = mAa + mBa

F – g sin θ(mA + mB) = (mA + mB)a

a = [F – g sin θ(mA + mB)]/(mA + mB)

a = [F/(mA + mB)] – g sin θ ............... Pers. (3)

Dengan mensubtitusikan nilai-nilai yang diketahui dalam soal ke dalam persamaan (3), maka kita peroleh besar percepatan kedua balok sebagai berikut.

a = [480/(40 + 20)] – (10) sin 37°

a = (480/60) – (10)(0,6)

a = 8 – 6

a = 2 m/s2

Jadi, besar percepatan kedua balok adalah 2 m/s2. Untuk menentukan gaya kontak antara balok A dan B, kita subtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (2) sebagai berikut.

FAB = mBa + mBg sin θ

FAB = (20)(2) + (20)(10)(sin sin 37°)

FAB = 40 + (200)(0,6)

FAB = 40 + 120

FAB = 160 N

Dengan demikian, besar gaya kontak antara balok A dan balok B adalah 160 N.

Kembali ke Bagian 1