Contoh Soal Dinamika Partikel (Gerak Translasi) dan Jawabannya Lengkap 2
https://www.fisikabc.com/2018/06/contoh-soal-dinamika-partikel-gerak-translasi-2.html?m=0
Daftar Materi Fisika
Advertisement
Baca Juga:
Contoh Soal Gaya Kontak di Bidang Miring:
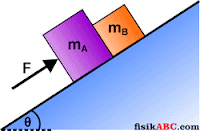
Balok A dan balok B terletak di atas permukaan bidang miring licin dengan sudut kemiringan 37°. Massa balok A 40 kg dan massa balok B 20 kg. Kemudian balok A didorong dengan gaya F sebesar 480 N seperti yang diperlihatkan pada gambar di bawah ini. Tentukan besar percepatan gerak kedua balok dan juga gaya kontak antara balok A dan balok B.
Jawab
Diketahui:
mA = 40 kg
mB = 20 kg
F = 480 N
θ = 37°
g = 10 m/s2
Ditanyakan: Percepatan dan gaya kontak.
Langkah pertama adalah menggambarkan diagram gaya yang bekerja pada masing-masing balok secara terpisah untuk mempermudah membedakan gaya-gaya mana yang bekerja pada kedua balok. Perhatikan gambar di bawah ini.

FAB adalah gaya aksi yang diberikan balok A kepada balok B, sedangkan FBA adalah gaya reaksi yang diberikan balok B kepada balok A. Kedua gaya tersebut merupakan gaya kontak yang besarnya sama. Lalu untuk menentukan besar percepatan kedua balok dan juga gaya kontak, kita tinjau persamaan gerak masing-masing balok menggunakan Hukum II Newton sebagai berikut.
∎ Tinjau Balok A
Karena bidang miring licin maka tidak ada gaya gesek yang bekerja, sehingga resultan gaya pada sumbu-Y tidak perlu diuraikan.
ΣFX = ma
F – wA sin θ – FBA = mAa
F – mAg sin θ – FBA = mAa ............... Pers. (1)
∎ Tinjau Balok B
ΣFX = ma
FAB – wA sin θ = mBa
FAB – mBg sin θ = mBa
FAB = mBa + mBg sin θ ............... Pers. (2)
Karena FAB = FBA, maka kita dapat mensubtitusikan persamaan (2) ke dalam persamaan (1) sebagai berikut.
F – mAg sin θ – (mBa + mBg sin θ) = mAa
F – mAg sin θ – mBa – mBg sin θ = mAa
F – mAg sin θ – mBg sin θ = mAa + mBa
F – g sin θ(mA + mB) = (mA + mB)a
a = [F – g sin θ(mA + mB)]/(mA + mB)
a = [F/(mA + mB)] – g sin θ ............... Pers. (3)
Dengan mensubtitusikan nilai-nilai yang diketahui dalam soal ke dalam persamaan (3), maka kita peroleh besar percepatan kedua balok sebagai berikut.
a = [480/(40 + 20)] – (10) sin 37°
a = (480/60) – (10)(0,6)
a = 8 – 6
a = 2 m/s2
Jadi, besar percepatan kedua balok adalah 2 m/s2. Untuk menentukan gaya kontak antara balok A dan B, kita subtitusikan nilai percepatan yang kita peroleh ke dalam persamaan (2) sebagai berikut.
FAB = mBa + mBg sin θ
FAB = (20)(2) + (20)(10)(sin sin 37°)
FAB = 40 + (200)(0,6)
FAB = 40 + 120
FAB = 160 N
Dengan demikian, besar gaya kontak antara balok A dan balok B adalah 160 N.
Contoh Soal Gerak Benda di Bidang Datar Licin:
Sebuah balok es yang memiliki massa 25 kg didorong Zeni dengan sudut 30°. Jika balok es bergerak dengan percepatan konstan sebesar 1/4√3 m/s2, maka tentukan besar gaya dorongan Zeni tersebut.
Jawab
Diketahui:
m = 25 kg
a = 1/4√3 m/s2
θ = 30°
Ditanyakan: gaya dorong (F)
Langkah pertama adalah menggambarkan diagram gaya yang bekerja pada objek. Seperti yang diperlihatkan pada gambar berikut ini.

Tentu kalian tahu kalau balok es permukaannya licin, sehingga kita dapat mengabaikan gaya gesek. Oleh karena tidak ada gaya gesek, maka kita tidak perlu menentukan resultan gaya pada sumbu-Y (vertikal). Berdasarkan Hukum II Newton, maka resultan gaya pada sumbu-X (horizontal) adalah sebagai berikut.
ΣFX = ma
F cos θ = ma
F cos 30° = (25)( 1/4√3)
F(1/2√3) = 25/4√3
F = (25/4√3)/(1/2√3)
F = 25/2
F = 12,5 N
Jadi, Zeni mendorong balok es tersebut dengan gaya sebesar 123,5 N.
Contoh Soal Gerak Benda di Bidang Datar Kasar:
Anis menarik sebuah balok yang bermassa 10 kg dengan gaya sebesar 100 N dengan arah membentuk sudut 37° terhadao lantai. Koefisien gesek statis dan kinetis benda terhadap lantai adalah 0,5 dan 0,4. Jika percepatan gravitasi di tempat itu adalah 10 m/s2. Maka tentukan bergerak atau tidak benda tersebut. jika bergerak tentukan percepatannya.
Jawab
Diketahui:
m = 10 kg
F = 100 N
θ = 37°
μs = 0,5
μk = 0,4
g = 10 m/s2
Ditanyakan: diam atau bergerak, jika bergerak berapa a.
Seperti biasa, langkah pertama adalah menggambarkan diagram gaya yang bekerja pada benda tersebut, seperti yang ditunjukkan pada gambar di bawah ini.

Langkah kedua adalah menentukan besar gaya normal N dengan menggunakan Hukum I Newton sebagai berikut.
ΣFY = 0
N + F sin θ – w = 0
N = w – F sin θ
N = mg – F sin θ
N = (10)(10) – (100)(sin 37°)
N = 100 – (100)(0,6)
N = 100 – 60
N = 40 N
Langkah selanjutnya adalah menghitung dahulu besar gaya gesek statis maksimumnya (fs maks) sebagai berikut.
fs maks = μsN
fs maks = (0,5)(40)
fs maks = 20 N
Karena F = 100 N > fs maks maka balok yang ditarik Anis sudah bergerak sehingga bekerja gaya gesek kinetik (fk). Dengan menggunakan Hukum II Newton, maka percepatan gerak balok adalah sebagai berikut.
ΣFX = ma
F cos θ – fk = ma
F cos θ – μkN = ma
(100)(cos 37°) – (0,4)(40) = 10a
(100)(0,8) – 16 = 10a
80 – 16 = 10a
64 = 10a
a = 6,4 m/s2
Jadi, balok tersebut bergerak dengan percepatan sebesar 6,4 m/s2.
Contoh Soal Gerak Benda di Bidang Miring Licin:
Sebuah balok yang massanya 6 kg meluncur ke bawah pada sebuah papan licin yang dimiringkan 30ᵒ dari lantai. Jika jarak lantai dengan balok 10 m dan besarnya percepatan gravitasi di tempat itu adalah 10 ms-2, maka tentukan percepatan dan waktu yang diperlukan balok untuk sampai di lantai.
Jawab
Diketahui:
m = 6 kg
s = 10 m
θ = 30ᵒ
g = 10 m/s
Ditanyakan: Percepatan dan waktu.
Langkah pertama untuk menyelesaikan soal yang berhubungan dengan dinamika gerak adalah menggambarkan skema ilustrasi soal beserta diagram gaya yang bekerja pada sistem seperti yang ditunjukkan pada gambar di bawah ini.

Karena kondisi bidang miring adalah licin, maka tidak ada gaya gesek sehingga kita tidak perlu menguraikan resultan gaya pada sumbu-Y atau sumbu vertikal. Menurut Hukum II Newton, resultan gaya yang bekerja pada benda dalam arah sumbu-X adalah sebagai berikut.
ΣFX = ma
w sin θ = ma
mg sin θ = ma
a = g sin θ …………… Pers. (1)
■ Menentukan percepatan
Untuk menentukan besar percepatan balok, subtitusikan nilai-nilai yang diketahui dalam soal ke persamaan (1) sebagai berikut.
a = g sin θ
a = (10)(sin 30ᵒ)
a = (10)(0,5)
a = 5 m/s2
jadi, balok tersebut meluncur ke bawah dengan percepatan sebesar 5 m/s2.
Important:
Rumus percepatan pada persamaan (1) berlaku untuk semua gerak benda di bidang miring licin tanpa gaya luar.
|
■ Menentukan waktu untuk sampai di lantai
Untuk menentukan waktu yang diperlukan balok untuk mencapai lantai, kita gunakan rumus jarak pada gerak lurus berubah beraturan atau GLBB. (Kenapa GLBB bukan GLB?).
s = v0t + ½ at2
karena tidak ada keterangan mengenai kecepatan awal, maka v0 = 0 sehingga
s = ½ at2
t2 = 2s/a
t = √(2s/a) …………… Pers. (2)
Subtitusikan besar percepatan dan nilai yang diketahui dalam soal ke persamaan (2)
t = √[(2)(10)/5]
t = √(20/5)
t = √4
t = 2 m/s2
Dengan demikian, waktu yang diperlukan balok untuk sampai ke lantai adalah 2 detik.
Contoh Soal Gerak Benda di Bidang Miring Kasar:
Sebuah benda bergerak menuruni bidang yang kemiringannya 37ᵒ terhadap bidang horizontal. Apabila besar koefisien gesek kinetik 0,1, maka tentukanlah percepatan dan kecepatan benda tersebut setelah bergerak selama 4 sekon.
Jawab
Diketahui:
θ = 37ᵒ
μk = 0,1
t = 4 s
g = 10 m/s
Ditanyakan: Percepatan dan kecepatan
Langkah pertama, kita gambarkan skema ilustrasi soal lengkap dengan diagram gaya yang bekerja pada sistem seperti yang diperlihatkan pada gambar di bawah ini.
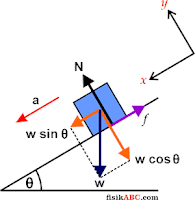
Berbeda dengan contoh soal sebelumnya, karena kondisi bidang miring kasar, maka resultan gaya pada sumbu-Y juga perlu diuraikan, tentunya kalian tahu alasannya. Dengan menggunakan Hukum II Newton, maka resultan gaya yang bekerja pada benda adalah sebagai berikut.
Resultan Gaya pada Sumbu-Y
ΣFY = ma
N – w cos θ = ma
Karena tidak terjadi gerak pada arah vertikal, maka a = 0 sehingga
N – w cos θ = 0
N – mg cos θ = 0
N = mg cos θ
Resultan Gaya pada Sumbu-X
ΣFX = ma
w sin θ – f = ma
mg sin θ – μkN = ma
mg sin θ – μkmg cos θ = ma
a = g sin θ – μkg cos θ …………… Pers. (3)
■ Menentukan percepatan
Untuk menentukan besar percepatan benda, subtitusikan nilai-nilai yang diketahui dalam soal ke persamaan (3) sebagai berikut.
a = g sin θ – μkg cos θ
a = (10)(sin 37ᵒ) – (0,1)(10)(cos 37ᵒ)
a = (10)(0,6) – (1)(0,8)
a = 6 – 0,8
a = 5,2 m/s2
jadi, besar percepatan benda tersebut adalah 5,2 m/s2.
Important:
Rumus percepatan pada persamaan (3) berlaku untuk semua gerak benda di bidang miring kasar tanpa gaya luar.
|
■ Menentukan kecepatan
Untuk menentukan besar kecepatan setelah 4 detik, kita gunakan rumus kecepatan pada gerak lurus berubah beraturan atau GLBB sebagai berikut.
v = v0 + at
karena tidak ada kecepatan awal, maka v0 = 0
v = at
v = (5,2)(4)
v = 20,8 m/s
Dengan demikian, besar kelajuan benda setelah bergerak selama 4 detik adalah 20,8 m/s.