3 Jenis Pemuaian Zat, Rumus, Contoh Soal dan Pembahasan
https://www.fisikabc.com/2018/05/3-jenis-pemuaian-zat.html
Daftar Materi Fisika
Advertisement
Baca Juga:
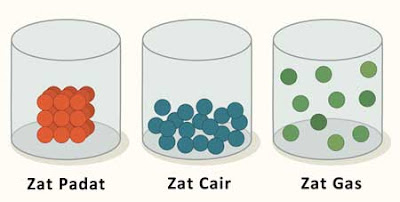
Suatu benda baik padat, cair, maupun gas terdiri atas partikel-partikel sangat kecil yang selalu bergetar disebut molekul. Jarak antarmolekulnya zat padat sangat berdekatan. Pada zat cair, jarak antarmolekulnya agak renggang, sedangkan pada gas jarak antarmolekulnya sangat renggang. Perhatikan gambar susunan partikel zat padat, cair dan gas berikut ini.
Jika suatu benda dipanaskan, molekul-molekul itu bergetar semakin cepat. Getaran antarmolekul tersebut menyebabkan molekul-molekul saling dorong. Akibat dorongan molekul tersebut, maka suatu benda akan mengalami proses pemuaian.
Nah, pada kesempatan kali ini kita akan mempelajari pemuaian pada 3 macam zat, yakni pemuaian zat padat, cair, dan gas. Untuk itu, silahkan kalian simak baik-baik penjelasan berikut ini. Selamat membaca dan belajar, semoga bisa paham.
1. Pemuaian Zat Padat
Pemuaian pada zat padat dapat diamati melalui perubahan panjang, luas dan volume. Sehingga dikenal pada zat padat dikenal pemuaian panjang, pemuaian luas dan pemuaian volume. Penjelasan dari ketiga jenis pemuaian zat padat tersebut adalah sebagai berikut.
#1 Pemuaian Panjang
Seutas kawat logam yang panjangnya l0 dan bersuhu T0 dipanaskan sampai suhu T maka kawat logam itu akan memuai sehingga panjangnya menjadi l. Perhatikan gambar ilustrasi pemuaian panjang pada kawat logam berikut ini.
∆l = l – l0 ……… Pers. (1)
Pertambahan panjang kawat dapat ditentukan dengan persamaan sebagai berikut.
∆l = αl0∆T …… Pers. (2)
Pada persamaan (2) tersebut, α (dibaca: alfa) adalah koefisien muai panjang. Dari persamaan (1) dan persamaan (2), maka kita peroleh persamaan berikut.
l – l0 = αl0∆T
l = l0 + αl0∆T
l = l0(1 + α∆T) atau l = l0[1 + α(T – T0)] …… Pers. (3)
|
Besar koefisien muai panjang beberapa bahan pada suhu 20oC diperlihatkan pada tabel berikut ini.
Tabel Koefisien Muai Panjang Berbagai Zat pada Suhu 20oC
Nama Zat
|
Koefisien Muai Panjang
α (/oC) |
Aluminium
|
2,5 × 10-5
|
Kuningan dan perunggu
|
1,9 × 10-6
|
Beton dan batu
|
≈ 1,2 × 10-5
|
Kaca (biasa)
|
9 × 10-6
|
Kaca (pyrex)
|
3 × 10-6
|
Timah
|
2,9 × 10-5
|
Besi
|
1,1 × 10-5
|
Kwarsa
|
0,4 × 10-6
|
Baja
|
1,2 × 10-5
|
Marmer
|
1,4 × 10-6 – 3,6 × 10-6
|
Tembaga
|
1,7 × 10-5
|
Kebutuhan pengetahuan mengenai koefisien muai panjang suatu bahan adalah untuk memperhitungkan penggunaan bahan tersebut. Misalnya, pemilihan bahan dan ukuran yang digunakan untuk konstruksi jembatan.
Pada salah satu ujung jembatan ini, dipasang roda dan diberi celah untuk memberi ruangan ketika jembatan memuai.
Pada salah satu ujung konstruksi jembatan modern, diberikan roda baja yang dapat berputar bebas. Ketika jembatan memuai akibat panas, dasar jembatan dapat menggerakkan roda baja tersebut. Pada ujung yang lain juga diberikan celah yang memungkinkan dasar jembatan dapat bergerak.
Contoh Soal Pemuaian Panjang
Pada suhu 20oC, panjang kawat besi adalah 20 m. Berapakah panjang kawat besi tersebut pada suhu 100oC jika koefisien muai panjang besi 1,1 × 10-5/oC?
Penyelesaian:
Diketahui:
T0 = 20oC
T = 100oC
l0 = 20 m
α = 1,1 × 10-5 C-1
Ditanyakan: l = …?
Jawab:
l = l0 [1 + α(T – T0)]
l = 20[1 + 1,1 × 10-5(100 – 20)]
l = 20[1 + 1,1 × 10-5(80)]
l = 20(1 + 8,8 × 10-4)
l = 20(1 + 0,00088)
l = 20(1,00088)
l = 20,0176 m
Jadi, panjang kawat besi tersebut pada suhu 100oC adalah 20,0176 m.
#2 Pemuaian Luas
Sekeping logam yang panjangnya x dan lebarnya y akan mengalami muai luas jika dipanaskan. Pemuaian luas suatu zat bergantung kepada koefisien muai luas yang diberi lambang atau simbol β (dibaca: beta). Muai luas terbentuk dari dua pemuaian, yaitu pertambahan panjang dan pertambahan lebar. Akibatnya, besar koefisien muai luas (β) sama dengan dua kali koefisien muai panjang (α), yaitu:
β = 2α …… Pers. (4)
jika sekeping logam yang luasnya A0 dan suhunya T0 dipanaskan sampai suhu T, logam tersebut akan memuai sehingga luasnya menjadi A. Besarnya pertambahan luas keping logam ∆A tersebut dapat dituliskan dalam persamaan berikut.
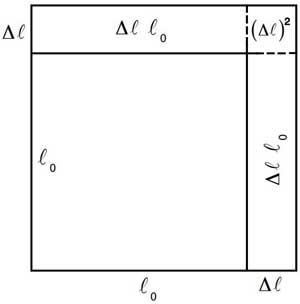
Misalnya, luas pesegi:
A0 = l02
∆l = αl0∆T
∆A = 2l0∆l
∆A = 2l0(αl0∆T)
∆A = 2αl02∆T
∆A = βA0∆T …… Pers. (5)
Dengan memasukkan harga ∆A = A – A0 maka persamaan (5) menjadi:
A – A0 = βA0∆T
A = A0(1 + β∆T) atau A = A0[1 + β(T – T0)] …… Pers. (6)
|
Contoh Soal Pemuaian Luas
Sekeping aluminium dengan panjang 40 cm dan lebar 30 cm dipanaskan dari 40oC sampai 140oC. Jika koefisien muai panjang aluminium tersebut (α) adalah 2,5 × 10-5 oC, tentuan luas keping aluminium setelah dipanaskan.
Penyelesaian:
Diketahui:
A0 = 40 cm × 30 cm = 1.200 cm2
β = 2α = 2(2,5 × 10-5 oC) = 5 × 10-5 oC
∆T = 140oC – 40oC = 100oC
Ditanyakan: A = …?
Jawab:
A = A0(1 + β∆T)
A = 1.200(1 + 5 × 10-5 × 100)
A = 1.200(1 + 5 × 10-3)
A = 1.200(1 + 0,005)
A = 1.200(1,005)
A = 1206 cm2
Jadi, luas penampang aluminium setelah dipanaskan adalah 1206 cm2.
#3 Pemuaian Volume
Pemuaian volume benda bergantung kepada koefisien muai volume yang diberi lambang atau simbol γ (dibaca: gamma). Pemuaian volume terbentuk dari tiga pemuaian, yaitu pertambahan panjang, pertambahan lebar, dan pertambahan tinggi. Akibatnya, besar koefisien muai volume (γ) sama dengan tiga kali koefisien muai panjang (α), yaitu:
γ = 3α …… Pers. (7)
Jika sebuah benda berbentuk balok yang volumenya V0 dan suhunya T0 dipanaskan sampai suhu T, benda tersebut akan memuai sehingga volumenya menjadi V.
Besarnya pertambahan volume benda berbentuk ruang dapat ditulis dalam bentuk persamaan berikut.
Misalnya, volume kubus.
V0 = l03
∆l = αl0∆T
∆V = 3l02∆l
∆V = 3l02(αl0∆T)
∆V = 3αl03∆T …… Pers. (8)
∆V = γV0∆T ……… Pers. (9)
Dengan memasukkan harga ∆V = V – V0 maka persamaan (9) menjadi:
V – V0 = γV0∆T
V = V0(1 + γ∆T) atau V = V0[1 + γ (T – T0)] …… Pers. (10)
|
Contoh Soal Pemuaian Volume
Sebuah besi bervolume 1 m3 dipanaskan dari 0oC sampai 1.000oC. Jika massa besi pada suhu 0oC adalah 7.200 kg dan koefisien muai panjangnya 1,1 ×10-5/oC, hitunglah massa jenis besi pada suhu 1.000oC.
Penyelesaian:
Diketahui:
V0 = 1 m3
γ = 3α = 3(1,1 × 10-5) = 3,3 × 10-5/oC
ρ = 7.200 kg/m3
∆T = 1000oC – 0oC = 1000oC
Ditanyakan: massa jenis besi setelah dipanaskan
Jawab:
□ Volume besi setelah dipanaskan adalah:
V = V0(1 + γ∆T)
V = 1[1 + (3,3 × 10-5)(1000)]
V = 1(1 + 3,3 × 10-2)
V = 1(1 + 0,033)
V = 1(1,033)
V = 1,033 m3
□ Setelah dipanaskan, volume benda berubah tetapi massanya tetap.
ρ
|
=
|
m
|
V
|
ρ
|
=
|
7200 kg
|
1,033 m3
|
ρ
|
=
|
6.969,99 kg/m3
|
Jadi, massa jenis besi menjadi 6.969,99 kg/m3.
2. Pemuaian Zat Cair
Pada umumnya, pemuaian zat cair hanya dapat diamati melalui perubahan volumenya. Jika sebuah bejana gelas yang berisi air hampir penuh dipanaskan, setelah kenaikan suhu, air akan tumpah. Peristiwa tersebut dapat diterangkan sebagai berikut.
Ruang gerak partikel pada zat cair lebih besar daripada ruang gerak partikel pada zat padat. Jika kedua zat itu mengalami pemanasan secara bersamaan, partikel pada zat cair lebih leluasa bergerak dibandingkan dengan partikel zat padat.
Oleh karena itu, volume air lebih cepat bertambah daripada volume bejana gelas sehingga air akan tumpah. Peristiwa tersebut menunjukkan bahwa koefisien muai volume zat cair lebih besar daripada koefisien muai volume zat padat.
Anomali Air
Telah kalian ketahui bahwa jika zat padat, zat cair, dan gas dipanaskan, zat-zat tersebut akan memuai seiring dengan kenaikan suhu. Pada pemanasan air, ada hal menarik yang dapat diamati. Misalkan, kalian memanaskan air bersuhu 0oC sebanyak 1,0002 cm3.
Di antara suhu 0oC dan 4oC, volume air akan menyusut, tetapi massanya tetap sehingga massa jenisnya naik. Jika pemanasan diteruskan sampai di atas 4oC, volume air akan memuai seperti zat-zat yang lain. Sifat pemuaian air yang tidak teratur ini disebut anomali air, seperti yang diperlihatkan grafik pada gambar berikut ini.
Dari grafik tersebut, tampak bahwa dari 0oC sampai 4oC volume air terus menyusut sampai kurang dari 1.000 cm3. Kemudian, di atas suhu 4oC volume air memuai.
Untuk massa yang sama, pada suhu 0oC volume es lebih besar daripada volume air. Berarti massa jenis es lebih kecil daripada massa jenis air karena massa jenis berbanding terbalik dengan volume (ρ = m/V). Itulah sebabnya, bongkahan es dapat mengapung di atas air.
3. Pemuaian Zat Gas
Pada tahun 1787, Jacques Charles melakukan percobaan yang menunjukkan bahwa semua gas memuai dengan koefisien muai yang sama, yaitu sebesar 1/273oC. Menurutnya, jika semua gas dipanaskan, volume dan tekanannya berubah.
#1 Pemuaian Gas pada Tekanan Tetap
Perhatikan gambar di bawah ini. Sebuah tabung kaleng, tutupnya diberi pipa kecil yang ujungnya dipasangi balon kempes. Jika tabung tersebut dipanaskan, suhu gas yang berada di dalam tabung akan naik.
Pada keadaan itu, partikel gas bergerak saling berdesakan ke segala arah dan masuk ke dalam balon melalui pipa sehingga balon membesar. Peristiwa tersebut menunjukkan telah terjadi pemuaian gas di dalam tabung pada tekanan tetap (sama dengan tekanan udara di luar tabung).
Grafik suhu terhadap volume pada proses pemanasan gas dengan tekanan tetap tampak seperti pada gambar berikut ini.
Dari gambar tersebut, tampak bahwa jika tekanan gas tetap, volume gas berbanding lurus dengan suhunya. Selanjutnya, pernyataan ini disebut Hukum Charles. Secara matematis ditulis sebagai berikut.
V = CT
V
|
=
|
V
|
atau
|
V1
|
=
|
V2
|
…… Pers. (11)
|
T
|
T1
|
T2
|
Keterangan:
V1 = volume awal (m3)
V2 = volume gas setelah dipanaskan (m3)
T1 = suhu awal (K)
T2 = suhu gas setelah dipanaskan (K)
Besarnya pertambahan volume gas saat dipanaskan memenuhi persamaan yang sama dengan besarnya pertambahan volume zat padat, yaitu sebagai berikut.
Vt = V0(1 + γ∆T) …… Pers. (12)
|
Oleh karena ∆T = T dan γ = 1/273 maka persamaan (12) dapat ditulis ulang sebagai berikut.
Vt
|
=
|
V0
|
1
|
+
|
1
|
∆T
|
…… Pers. (13)
|
273
|
#2 Pemuaian Gas pada Volume Tetap
Perhatikan gambar di bawah ini. Pada bagian ujung pipa ditutup rapat dengan sumbat paralon. Jika tabung pada gambar tersebut dipanaskan, volume gas tetap. Akibatnya, tekanan gas bertaambah besar. Jadi pada pemanasan ini volume gas tetap, sedangkan tekanannya berubah.
Kalian dapat mengetahui hubungan antara kenaikan suhu dan tekanan pada pemanasan gas pada volume tetap dengan melakukan percobaan berikut.
Percobaan: Hubungan Suhu dan Tekanan
Tujuan Percobaan:
Mengetahui hubungan antara kenaikan suhu dan tekanan.
Alat-Alat Percobaan:
Alat ukur Bourdon, termometer raksa, tabung gas, pembakar bunsen, dan kaki tiga.
Langkah-Langkah Percobaan:
1. Rancanglah peralatan tersebut seperti pada gambar berikut ini. Pastikan tidak ada kebocoran gas dalam tabung.
2. Setelah terjadi kesetimbangan termal antara termometer dan gas dalam tabung, catat suhu awal gas (terlihat pada termometer) dan tekanan udara (terlihat pada alat Bourdon).
3. Panaskan tabung dengan pembakar bunsen. Catat kenaikan suhu udara dan tekanan udara dalam tabung pada suatu tabel.
4. Dari tabel tersebut, buatlah grafik suhu terhadap tekanan gas.
5. Buatlah kesimpulan dari kegiatan ini.
Percobaan serupa dengan eksperimen di atas pernah dilakukan oleh para ahli Fisika. Dari hasil percobaan yang telah mereka lakukan, diperoleh grafik tekanan gas terhadap suhu pada volume tetap berbentuk garis lurus seperti yang diperlihatkan pada gambar berikut ini.
Secara matematis, garis lurus pada grafik tersebut memenuhi persamaan berikut.
P = CT
P
|
=
|
C
|
atau
|
P1
|
=
|
P2
|
…… Pers. (14)
|
T
|
T1
|
T2
|
Keterangan:
P = tekanan gas (atm)
T = suhu gas (K)
C = konstanta
Dari persamaan P = CT diketahui bahwa tekanan gas berbanding lurus dengan suhunya pada volume tetap. Selanjutnya, pernyataan tersebut disebut Hukum Gay-Lussac.