Contoh Soal Perkalian Vektor Titik (Dot Product) dan Pembahasannya
https://www.fisikabc.com/2018/03/contoh-soal-perkalian-titik-vektor.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Seperti yang telah kalian ketahui, operasi vektor tidak hanya terbatas pada penjumlahan dan pengurangan vektor saja, operasi perkalian juga berlaku pada vektor. Perkalian vektor dibedakan menjadi tiga macam, antara lain perkalian vektor dengan skalar, perkalian titik (dot product), dan perkalian silang (cross product).
Nah, pada kesempatan kali ini kita akan mempelajari beberapa contoh soal tentang perkalian titik. Namun sebelum itu, kita ulas sedikit mengenai konsep perkalian titik (dot product) vektor berikut ini.
Perkalian Titik Vektor (Dot Product)
Perkalian titik antara dua vektor A dan vektor B merupakan besaran skalar yang besarnya sama dengan hasil kali kedua vektor itu terhadap cosinus sudut apitnya. Perhatikan gambar di bawah ini.
θ adalah sudut apit antara dua vektor. Perkalian titik antara vektor A dan B dituliskan sebagai berikut.
A . B = |A||B| cos θ
Keterangan:
θ = sudut yang dibentuk oleh dua vektor A dan B dengan 0o ≤ θ ≤ 180o
|A| = besar vektor A
|B| = besar vektor B
AB cos θ = BA cos θ maka A . B = B . A. Perkalian titik dua vektor disebut juga sebagai perkalian skalar.
Untuk memudahkan perhitungan perkalian titik dua vektor, perlu dipahami sifat-sifat perkalian titik sesama vektor. Perkalian titik antara dua vektor satuan akan bernilai satu jika kedua vektor tersebut sejenis dan bernilai nol jika kedua vektor tersebut tidak sejenis.
i . i = j . j = k . k = (1) (1) cos 0o = 1
i . j = i . k = j . k = (1) (1) cos 90o = 0
Sudut antara vektor satuan i dan i adalah 0o maka (i) (i) cos 0o = 1, sedangkan sudut antara vektor satuan i dan j adalah 90o maka (i) (j) cos 90o = 0. Ketentuan ini memenuhi sifat perkalian titik sesama vektor. Secara matematis, perkalian titik vektor A dan B dapat diperoleh sebagai berikut.
A . B = (Axi + Ayj + Azk) . (Bxi + Byj + Bzk)
A . B = AxBx + AyBy + AzBz
Contoh Soal:
Vektor gaya dan perpindahan mempunya persamaan F = (i + j + k) N dan s = (3i + 4j + 6k) m. tentukan usaha yang dilakukan oleh gaya!
Penyelesaian:
Diketahui:
F = (i + j + k)
s = (3i + 4j + 6k)
ditanya: usaha (W)
Jawab:
Usaha merupakan hasil perkalian titik antara gaya dengan perpindahan, jadi
W = F . s
W = (i + j + k) . (3i + 4j + 6k)
W = (1)(3) + (1)(4) + (1)(6)
W = 3 + 4 + 6
W = 13
Jadi usaha yang dilakukan oleh gaya tersebut adalah 13 joule.
Contoh Soal dan Pembahasan
1. Tentukan hasil perkalian titik antara dua vektor satuan A = 2i + 3j + 5k dan B = 4i + 2j – k
Jawab:
A . B = AxBx + AyBy + AzBz
A . B = (2)(4) + (3)(2) + (5)(-1)
A . B = 8 + 6 – 5
A . B = 9
2. Balok yang berada pada bidang datar licin ditarik oleh gaya 200 N dengan arah membentuk sudut 60o terhadap arah horizontal seperti pada gambar di bawah ini.
Pada saat balok berpindah 8 m maka tentukan usaha yang dilakukan oleh gaya F.
Penyelesaian:
Usaha dapat didefinisikan sebagai perkalian titik gaya yang bekerja selama perpindahannya dengan perpindahannya tersebut. Berarti dapat diperoleh hubungan sebagai berikut.
W = F . s
W = |F||s| cos 60o
W = (200)(8)(1/2)
W = 800 joule
Usaha merupakan besaran skalar.
3. Tentukanlah hasil perkalian titik antara dua vektor satuan A = i + 2j + 3k dan B = 3i + 2j – k
Jawab:
A . B = AxBx + AyBy + AzBz
A . B = (1)(3) + (2)(2) + (3)(-1)
A . B = 3 + 4 – 3
A . B = 4
4. Diketahui 2 buah vektor yaitu sebagai berikut
a = 4i + 3j – k
b = -i – 2j + 3k
Hitunglah sudut antara vektor a dan vektor b.
Penyelesaian:
Besar vektor a adalah sebagai berikut.
|a| = √[(4)2 + (3)2 + (-1)2]
|a| = √(16 + 9 + 1)
|a| = √26
Besar vektor b adalah sebagai berikut
|b| = √[(-1)2 + (-2)2 + (3)2]
|b| = √(1 + 4 + 9)
|b| = √14
Besar perkalian titik vektor a . b adalah sebagai berikut.
a . b = AxBx + AyBy + AzBz
a . b = (4)(-1) + (3)(-2) + (-1)(3)
a . b = -4 – 6 – 3
a . b = -13
Karena perkalian titik menghasilkan besaran skalar, maka nilai perkalian titik harus selalu positif, sehingga
a . b = 13
Dengan menggunakan perkalian titik, maka sudut antara vektor a dan b adalah sebagai berikut.
a . b = |a||b| cos θ
13 = (√26)(√14) cos θ
13 = √364 cos θ
13 = 19 cos θ
cos θ = 13/19
cos θ = 0,68
θ = arc cos 0,68
θ = 47o
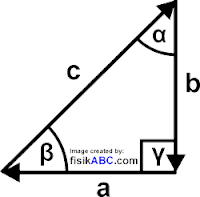
5. Diketahui vektor a, b, dan c seperti pada gambar di bawah ini. Besar vektor-vektor tersebut masing-masing 3, 4, dan 5 satuan. Tentukanlah:
a) a . b
b) a . c
c) b . c
Jawab:
a) a . b = |a||b| cos γ
⇒ a . b = (3)(4) cos 90o
⇒ a . b = (12)(0)
⇒ a . b = 0
b) a . c = |a||c| cos (180o – β)
⇒ a . c = |a||c| (-cos β)
⇒ a . c = (3)(5)(-3/5)
⇒ a . c = (15)(-3/5)
⇒ a . c = -9
c) b . c = |b||c| cos (180o – α)
⇒ b . c = |b||c| (-cos α)
⇒ b . c = (4)(5)(-4/5)
⇒ b . c = (20)(-4/5)
⇒ b . c = -16
6. Diketahui tiga vektor berikut.
x = 2i + 3j
y = 3i + 2j
z = i + j + k
Hitunglah:
a) x . x
b) (x + y) . z
Jawab:
a) x . x = (2i + 3j) . (3i + 2j)
⇒ x . x = (2)(3) + (3)(2)
⇒ x . x = 6 + 6
⇒ x . x = 12
b) Pertama kita tentukan dahulu operasi penjumlahan yang berada di dalam tanda kurung, yaitu sebagai berikut.
⇒ x + y = (2i + 3j) + (3i + 2j)
⇒ x + y = 5i + 5j
Lalu hasilnya kita kalikan dengan vektor z, yaitu sebagai berikut.
(x + y) . z = (5i + 5j) . (i + j + k)
(x + y) . z = (5)(1) + (5)(1) + (0)(1)
(x + y) . z = 5 + 5 + 0
(x + y) . z = 10


terimakasih atas bantuannya jadi saya lebih faham dengan pelajaran fisika
ReplyDeleteterimakasih penjelasannya
ReplyDeletemohon maaf, saya ingin bertanya yang nomo 6 itu kan x.x = (2i + 3j).(3i + 2j)
ReplyDeletekenapa tidak (2i + 3j).(2i + 3j)
mungkin maksudnya x.y
Delete