Cara Penjumlahan Vektor Secara Grafis dan Analitis Serta Contohnya
https://www.fisikabc.com/2018/02/penjumlahan-vektor-secara-grafis-dan-analitis.html?m=1
Daftar Materi Fisika
Advertisement
Baca Juga:
Seperti yang telah kalian ketahui bahwa salah satu sifat vektor adalah dapat dijumlahkan. Lalu bagaimana caranya menjumlahkan vektor itu? Secara umum terdapat dua metode dalam penjumlahan vektor yaitu metode grafis dan metode analitis. Tahukah kalian apa perbedaan antara metode grafis dan metode analisis tersebut?
Metode grafis adalah cara melukiskan penjumlahan dua vektor atau lebih berdasarkan besar dan aranya membentuk suatu bidang datar. Jadi, dengan menggunakan metode grafis kita hanya bisa menggambarkan hasil penjumlahan atau resultan vektor tanpa tahu besar dan aranya secara kuantitatif. Metode grafis dibedakan menjadi tiga macam, yaitu metode segitiga, poligon dan jajar genjang.
Metode analitis adalah adalah cara melukiskan dan menentukan hasil penjumlahan vektor (resultan) melalui proses penguraian vektor menjadi vektor-vektor komponennya. Jadi, dengan menggunakan metode analitis kita tidak hanya mengetahui resultan vektor secara grafis tetapi juga dapat mengetahui besar dan arah vektor resultan secara kuantitatif.
Penjumlahan Vektor Secara Grafis
Seperti yang telah dijelaskan sebelumnya, metode grafis ada tiga jenis yaitu metode segitiga, metode poligon, dan metode jajarangenjang. Nah, berikut ini penjelasan mengenai cara menjumlahkan vektor dengan menggunakan ketiga macam metode grafis tersebut. Sebagai acuan diberikan 4 buah vektor dengan besar dan arah seperti pada gambar di bawah ini.
1. Cara Menjumlahkan Vektor dengan Metode Segitiga
Metode segitiga adalah cara penjumlahan dua vektor dengan memindahkah titik tangkap salah satu vektor ke ujung vektor lainnya kemudian menarik garis lurus dari pangkal ke ujung vektor tersebut. Garis lurus ini merupakan hasil penjumlahan vektor atau vektor resultan.
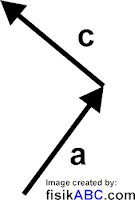
Misalkan kita akan menjumlahkan vektor a dan vektor c. Maka dengan menggunakan metode segitiga, langkah-langkahnya adalah sebagai berikut.
Langkah 1: gambarlah vektor a dan vektor c di mana titik tangkap atau titik pangkal vektor c berapa di ujung vektor a seperti yang diperlihatkan pada gambar berikut ini.
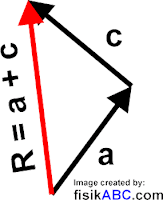
Langkah 2: gambarlah sebuah vektor dimulai dari titik tangkap vektor a menuju ujung vektor c. Vektor ini adalah vektor hasil penjumlahan a + c atau disebut sebagai vektor resultan yang dilambangkan dengan R seperti yang diperlihatkan pada gambar berikut ini.
Jika kalian perhatikan, ketiga vektor tersebut membentuk bangun segitiga. Oleh karena itu metode penjumlahan vektor seperti ini disebut dengan metode segitiga. Metode segitiga hanya dapat digunakan untuk melukiskan penjumlahan dua buah vektor saja, untuk penjumlahan vektor yang lebih banyak, maka bisa menggunakan metode poligon atau jajaran genjang.
2. Cara Menjumlahkan Vektor dengan Metode Poligon
Metode poligon adalah cara penjumlahan tiga atau lebih vektor dengan saling menghubungkan pangkal vektor yang satu ke ujung vektor yang lain sedemikian rupa hingga vektor terakhir. Kemudian menarik garis lurus dari pangkal vektor pertama menuju vektor terakhir. Garis lurus inilah yang disebut sebagai hasil penjumlahan vektor atau resultan vektor.
Misalkan kita akan menjumlahkan vektor a, b, c dan d. Maka dengan menggunakan metode poligon, langkah-langkahnya adalah sebagai berikut.
Langkah 1: gambarlah vektor a, b, c dan d di mana pangkal vektor b berada di ujung vektor a, pangkal vektor c berada di ujung vektor b dan pangkal vektor d berada di ujung vektor c seperti yang diperlihatkan pada gambar di bawah ini.
Langkah 2: gambarlah sebuah vektor yang dimulai dari titik tangkap atau pangkal vektor a dan menuju ujung vektor d. Vektor ini merupakan hasil penjumlahan vektor a + b + c + d atau disebut vektor resultan R seperti yang diperlihatkan pada gambar berikut ini.
Poligon adalah nama lain dari segi banyak atau bangun datar yang memilik sisi banyak (lebih dari tiga). Jadi, metode poligon pada penjumlahan vektor akan membentuk suatu bangun segi banyak. Metode poligon lebih unggul daripada metode segitiga, karena dapat menjumlahkan lebih dari dua vektor.
3. Cara Menjumlahkan Vektor dengan Metode Jajargenjang
Metode jajar genjang adalah cara menjumlahkan dua vektor atau lebih dengan menghubungkan pangkal vektor yang satu dengan pangkal vektor yang lain. Kemudian menarik sebuah garis lurus dan pangkal kedua vektor menuju pertemuan proyeksi masing-masing vektor. Garis ini adalah vektor resultan.
Misalkan kita akan menjumlahkan vektor a, b dan d. Maka dengan menggunakan metode jajargenjang, langkah-langkahnya adalah sebagai berikut.
Langkah 1: gambarlah vektor a dan b terlebih dahulu di mana pangkal masing-masing vektor saling bertemu. Kemudian proyeksikan vektor a di ujung vektor b dan proyeksikan vektor b di ujung vektor a. Gambarkan proyeksi vektor a dan b dalam bentuk garis putus-putus. Vektor a, vektor b beserta proyeksinya akan membentuk bangun jajar genjang seperti yang diperlihatkan pada gambar berikut.
Langkah 2: tarik vektor dari titik pengkal vektor a dan vektor b menuju titik pertemuan proyeksi kedua vektor. Vektor ini adalah hasil penjumlahan atau vektor resultan dari a + b seperti yang diperlihatkan pada gambar di bawah ini.
Langkah 3: gambar vektor d dengan pangkalnya berada di pangkal vektor a + b. Proyeksikan vektor d dan vektor a + b seperti pada langkah 1. Lalu tarik vektor dari pangkal vektor a + b dan vektor d menuju titik pertemuan proyeksi kedua vektor. Vektor akhir inilah yang merupakan hasil penjumlahan vektor a + b + d seperti yang diperlihatkan pada gambar berikut ini.
Metode jajar genjang lebih unggul dibandingkan dengan metode segitiga maupun poligon. Hal ini dikarenakan metode jajargenjang dapat digunakan untuk menjumlahkan dua vektor atau lebih. Meskipun demikian, metode jajargenjang tidak dapat menentukan besar dan arah vektor resultan secara kuantitatif.
Inilah yang menjadi ciri khusus metode grafis, yaitu hanya dapat digunakan untuk menggambarkan penjumlahan vektor tanpa dapat menghitung besar dan arah vektor resultannya. Oleh karena itu, agar dapat menentukan besar dan arah resultan vektor secara kuantitatif, maka digunakanlah metode analitis.
Penjumlahan Vektor Secara Analitis
Metode analitis disebut juga metode penguraian yaitu cara menjumlahkan vektor dengan memproyeksikan vektor-vektor pada sumbu-X dan sumbu-Y diagram cartesian. Lalu komponen-komponen vektor pada masing-masing sumbu dijumlahkan secara biasa.
Vektor komponen yang arahnya ke kanan atau ke atas bernilai positif, sedangkan vektor komponen yang arahnya ke bawah bernilai negatif. Misalkan diberikan tiga buah vektor dengan besar dan arahnya diperlihatkan seperti pada gambar berikut ini.
Dengan menggunakan metode analisis, maka penjumlahan vektor a + b + c dapat dilakukan melalui langkah-langkah sebagai berikut.
Langkah 1: gambarlah diagram cartesius, lalu lukis vektor a, b dan c pada bidang cartesius tersbeut dengan pangkal masing-masing vektor berada di pusat koordinat seperti yang diperlihatkan pada gambar di bawah ini.
Langkah 2: uraikan atau proyeksikan vektor a, b dan c ke dalam sumbu-X dan sumbu-Y sehingga akan terbentuk vektor komponan ax, ay, bx, by, cx, dan cy. Dalam hal ini, karena vektor c berhimpit pada sumbu-Y, maka vektor c tidak memiliki vektor komponen pada sumbu-X dan komponen vektor pada sumbu-Y yaitu cy = c. Supaya lebih jelas, perhatikan gambar berikut ini.
Langkah 3: setelah semua vektor komponen terbentuk, selanjutnya adalah menjumlahkan vektor komponen yang berada pada sumbu-X dan sumbu-Y yaitu sebagai berikut.
ΣRX = aX - bX
ΣRY = aY + bY + c
Kemudian, untuk menentukan besar vektor resultan maka dapat kalian pergunakan rumus berikut ini.
R = √[(ΣRX)2 + (ΣRY)2]
Sedangkan arah vektor resultan dapat dihitung dengan menggunakan rumus berikut.
tan α
|
=
|
ΣRY
|
ΣRX
|









Bingungin coeg!!!!!!
ReplyDeletemasa sih?
DeleteThis comment has been removed by the author.
ReplyDeleteLoh kok yg vektor analitis cuman ada satu? Harunyakan 2:dgn rumus kosinusnya mana?
ReplyDeleteAda kok, silahkan pelajari artikel ini
Deletehttps://www.fisikabc.com/2017/04/rumus-cepat-menghitung-vektor-resultan.html
Penjumlahan vektor dgn rumus cosinus nya mana nih?
ReplyDeleteAda di sini
Deletehttps://www.fisikabc.com/2017/04/rumus-cepat-menghitung-vektor-resultan.html
Ajarin masih bingung nih
ReplyDeleteDi bagian mana yg masih bingung?
DeleteKurang paham:(
ReplyDeleteAyo semangat pelajari lgi kk Fuji
Delete