Perbesaran Lup untuk Mata Berakomodasi pada Jarak Tertentu, Rumus, Gambar, Contoh Soal dan Pembahasan

Daftar Materi Fisika

• 1. Besaran Fisika
• 2. Vektor dan Resultan
• 3. Mekanika (Kinematika dan Dinamika)
• 4. Fisika Optik
• 5. Suhu dan Kalor

Advertisement

Baca Juga:

Untuk dapat melihat benda-benda kecil agar tampak lebih besar daripada ukuran sebenarnya, digunakan lup. Lup merupakan lensa cembung atau lensa positif. Sebagaimana kalian ketahui, lensa cembung memiliki kemampuan membentuk bayangan maya yang diperbesar jika benda terletak di antara titik fokus dan lensa.

Untuk lup atau kaca pembesar,benda selalu diletakkan dalam ruang I sehingga bayangan akan terletak di ruang (IV). Bayangan yang terletak di ruang (IV) bersifat maya dan tegak sehingga jarak bayangan yang dibentuk lup selalu negatif (s’ bertanda negatif).

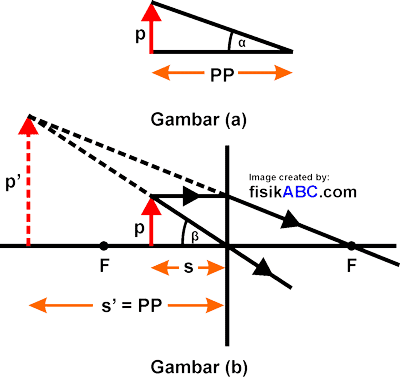
Pada saat menggunakan lup, jarak benda diubah-ubah sedemikian rupa sehingga didapatkan bayangan yang paling jelas bagi jenis mata normal atau emetropi, yaitu pada jarak baca yang biasanya sejauh 25 cm. Perhatikan gambar di bawah ini.

Keterangan gambar:

Gambar (a): sudut penglihatan mata (α), ketika benda dilihat tidak menggunakan lup.

Gambar (b): sudut penglihatan mata (β), ketika benda dilihat dengan menggunakan lup.

Perhatikan gambar (a) dan gambar (b) di atas. Tanpa lup, benda terlihat oleh mata dengan sudut α. Adapun jika menggunakan lup, benda terlihat oleh mata dengan sudut β sehingga perbesaran angulernya sebesar:

Manguler	=	tan β	………. Pers. (1)
		tan α

Jika sudut α dan β sangat kecil, maka tan α = α dan tan β = β sehingga persamaan (1) menjadi:

Manguler	=	β	………. Pers. (2)
		α

Oleh karena β = p’/s’ dan α = p/pp, β = p’/s’ = p/s maka persamaan (2) menjadi:

Manguler	=		p				PP		=	PP	………. Pers. (3)
			s				p			s

Jika mata berakomodasi pada jarak s’ = −x (maya), diperoleh persamaan sebagai berikut.

1	−	1	=	1	⇒	1	=	1	+	1
s		x		f		s		x		f

s	=	xf	………. Pers. (4)
		x + f

Jika persamaan (4) disubtituskan ke persamaan (3), akan diperoleh:

Manguler	=	PP (x + f)	=	PPx	+	PPf
		xf		xf		xf

Manguler	=	PP	+	PP
		f		x

Keterangan:

Manguler = perbesaran anguler

PP = Punctum Proximum atau titik dekat mata

f = jarak fokus lup

x = jarak antara bayangan yang terbentuk oleh lup

Rumus di atas adalah rumus perbesaran anguler lup untuk mata berakomodasi pada jarak tertentu yaitu sejauh x. Untuk memahami penggunaan rumus perbesaran sudut lup untuk mata berakomodasi pada jarak tertentu, silahkan kalian pelajari beberapa contoh soal dan pembahasannya berikut ini.

Contoh Soal 1:

Sebuah lup memiliki jarak fokus 6 cm. Hitunglah perbesaran lup jika mata melihat benda dengan berakomodasi pada jarak 25 cm.

Penyelesaian:

Diketahui:

PP = 25 cm (untuk mata normal)

f = 6 cm

x = 25 cm

Ditanyakan: Manguler

Jawab:

Perbesaran anguler lup dihitung untuk mata berakomodasi pada jarak 25 cm dihitung dengan menggunakan persamaan berikut.

Manguler	=	PP	+	PP
		f		x

Manguler	=	25	+	25
		6		25

Manguler = 4,17 + 1 = 5,17

Jadi, perbesaran anguler lup untuk penggunaan mata berakomodasi pada jarak 25 cm adalah 5,17 kali.

Contoh Soal 2:

Seseorang mengamati sebuah benda dengan menggunakan lup berkekuatan 10 dioptri. Apabila titik dekat mata orang tersebut adalah 25 cm, berapakah perbesaran lup itu jika mata berakomodasi pada jarak 50 cm?

Penyelesaian:

Diketahui:

PP = 25 cm

P = 10 dioptri → 1/f = 10, maka f = 0,1 m = 10 cm

x = 50 cm

Ditanyakan: Manguler ketika mata berakomodasi pada jarak 50 cm.

Jawab:

Perbesaran anguler lup dihitung untuk mata berakomodasi pada jarak 50 cm dihitung dengan menggunakan persamaan berikut.

Manguler	=	PP	+	PP
		f		x

Manguler	=	25	+	25
		10		50

M = 2,5 + 0,5 = 3

Jadi, perbesaran anguler lup untuk penggunaan mata berakomodasi pada jarak 50 cm adalah 3 kali.