Contoh Soal dan Pembahasan Sistem Katrol Materi Dinamika Translasi 2.1
https://www.fisikabc.com/2017/09/contoh-soal-sistem-katrol-materi-dinamika-translasi-2.1.html?m=1
Daftar Materi Fisika
Advertisement
Baca Juga:
Contoh Soal #2
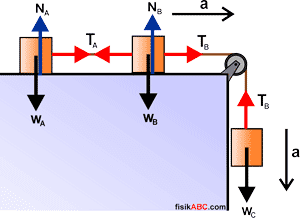
Dari susunan benda-benda pada gambar di bawah ini, tentukan besar percepatan benda dan tegangan setiap tali apabila mA = 10 kg, mB = 4 kg dan mC = 6 kg serta bidang licin (g = 10 m/s2).
Penyelesaian:
Diketahui:
mA = 10 kg
mB = 4 kg
mC = 6 kg
g = 10 m/s2
Ditanyakan: Percepatan dan gaya tegangan setiap tali.
Jawab:
Dari data di atas, meskipun mA + mB > mC, tetapi sistem tetap bisa bergerak. Hal ini dikarenakan kondisi bidang licin sehingga tidak ada gaya gesek yang menghambat gerak sistem. Untuk menentukan besar percepatan dan tegangan tali, langkah pertama adalah menggambarkan diagram atau garis-garis gaya yang bekerja pada sistem seperti yang diperlihatkan pada gambar berikut ini.
Dari gambar diagram gaya di ata, terdapat dua gaya tegangan tali yang tentu saja nilainya berbeda. TA adalah gaya tegangan tali yang bekerja antara benda A dan benda B sedangkan TB adalah gaya tegangan tali yang bekerja antara benda B dan benda C. Untuk menentukan besar percepatan sistem dan gaya tegangan tiap tali, kita tentukan resultan gaya pada masing-masing benda menggunakan Hukum II Newton sebagai berikut.
Tinjau Benda A
ΣFX = ma
TA = mAa …………… Pers. (1)
Tinjau Benda B
ΣFX = ma
TB – TA = mBa …………… Pers. (2)
Subtitusikan persamaan (1) ke persamaan (2)
TB – mAa = mBa
TB = mAa + mBa …………… Pers. (3)
Tinjau Balok C
ΣFY = ma
wC – TB = mCa
mCg – TB = mCa …………… Pers. (4)
Subtitusikan persamaan (3) ke persamaan (4)
mCg – (mAa + mBa) = mCa
mAa + mBa + mCa = mCg
(mA + mB + mC)a = mCg
a = mCg/(mA + mB + mC) …………… Pers. (5)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (5)
a = (6)(10)/(10 + 4 + 6)
a = 60/20
a = 3 m/s2
Jadi besar percepatan ketiga benda adalah 3 m/s2. Untuk menentukan besar gaya tegangan tali antara benda A dan benda B serta tegangan tali antara benda B dan benda C, kita masukkan nilai percepatan yang baru saja kita peroleh ke dalam persamaan (1) dan persamaan (3) sebagai berikut.
Tegangan Tali antara Benda A dan Benda B
TA = mAa
TA = (10)(3)
TA = 30 N
Jadi besar gaya tegangan tali yang terjadi antara benda A dan benda B adalah 30 N.
Tegangan Tali antara Benda B dan Benda C
TB = mAa + mBa
TB = (10)(3) + (4)(3)
TB = 30 + 12
TB = 42 N
Jadi besar gaya tegangan tali yang terjadi antara benda B dan benda C adalah 42 N.
Contoh Soal #3
Benda 1 bermassa m1 = 3 kg dan benda 2 bermassa m2 = 2 kg. Benda 2 mula-mula diam kemudian bergerak ke bawah sehingga menyentuh lantai yang jaraknya s dari benda 2. Meja kasar dengan koefisien gesek kinetis 0,25, percepatan gravitasi g = 10 m/s2 dan s = 5 m, maka tentukanlah waktu yang diperlukan benda 2 untuk menyentuh lantai.
Penyelesaian:
Diketahui:
m1 = 3 kg
m2 = 2 kg
μk = 0,25
g = 10 m/s2
s = 5 m
Ditanyakan: Waktu mencapai lantai.
Jawab:
Untuk mengetahui waktu yang diperlukan benda 2 untuk menyentuh lantai, maka besaran pertama yang harus kita tentukan adalah percepatan. Namun sebelum itu, kita gambarkan diagram gaya yang bekerja pada sistem seperti yang ditunjukkan oleh gambar berikut ini.
Dari gambar diagram gaya di atas, kita tentukan resultan gaya dengan meninjau gerak masing-masing benda menggunakan Hukum II Newton sebagai berikut.
Tinjau Benda 1
ΣFY = ma
N – w1 = m1a
N – m1g = m1a
Karena tidak terjadi gerak dalam arah vertikal, maka a = 0 sehingga
N – m1g = 0
N = m1g
ΣFX = ma
T – f = m1a
T – μkN = m1a
T – μkm1g = m1a
T = m1a + μkm1g …………… Pers. (6)
Tinjau Benda 2
ΣFY = ma
w2 – T = m2a
m2g – T = m2a …………… Pers. (7)
Subtitusikan persamaan (6) ke persamaan (7)
m2g – (m1a + μkm1g) = m2a
m1a + m2a = m2g – μkm1g
(m1 + m2)a = (m2 – μkm1)g
a = (m2 – μkm1)g/(m1 + m2) …………… Pers. (8)
Masukkan nilai-nilai yang diketahui dalam soal ke persamaan (8)
a = [2 – (0,25)(3)]10/(3 + 2)
a = (2 – 0,75)10/5
a = 12.5/5
a = 2,5 m/s2
Jadi besar percepatan kedua benda adalah 1,6 m/s2. Kemudian dalam menentukan waktu yang diperlukan benda 2 untuk menyentuh tanah, kita bisa gunakan rumus jarak pada gerak lurus berubah beraturan (GLBB) sebagai berikut.
s = v0t + ½ at2
Karena benda 2 mula-mula diam, maka tidak ada kecepatan awal sehingga v0 = 0. Jadi rumus di atas menjadi.
s = ½ at2
t2 = 2s/a
t = √(2s/a)
Kita masukkan harga percepatan dan nilai-nilai yang diketahui dalam soal ke dalam rumus di atas sehingga kita peroleh
t = √[2(5)/2,5]
t = √(10/2,5)
t = √4
t = 2 s
Dengan demikian, waktu yang diperlukan benda 2 untuk menyentuh tanah adalah 2 detik.
Demikianlah artikel tentang contoh soal dan pembahasan sistem katrol materi dinamika translasi bagian kedua. Kalian juga dapat mempelajari contoh soal dan pembahasan untuk model-model sistem katrol yang lain. Total ada 12 model katrol yang bisa kalian temukan dalam daftar berikut ini. Silahkan pilih dan klik link yang disajikan.
Bagian 1
Daftar Model Sistem Katrol, Materi dan Contoh Soal
No
|
Model Katrol
|
Materi
|
Contoh Soal
|
1
| |||
2
| |||
3
| |||
4
| |||
5
| |||
6
| |||
7
| |||
8
| |||
9
|
| ||
10
| |||
11
| |||
12
|















Post a Comment
Mohon berkomentar secara bijak dengan bahasa yang sopan dan tidak keluar dari topik permasalahan dalam artikel ini. Dan jangan ikut sertakan link promosi dalam bentuk apapun.
Terimakasih.