Rumus Tegangan Tali Pada Gerak Melingkar Vertikal, Contoh Soal dan Pembahasan

Daftar Materi Fisika

• 1. Besaran Fisika
• 2. Vektor dan Resultan
• 3. Mekanika (Kinematika dan Dinamika)
• 4. Fisika Optik
• 5. Suhu dan Kalor

Advertisement

Baca Juga:

Pernahkah kalian berkunjung ke Dunia Fantasi Taman Impian Jaya Ancol, di Jakarta Utara? Di tempat tersebut banyak dijumpai wahana permainan yang menerapkan prinsip gerak melingkar vertikal seperti Swing Boat (kora-kora atau perahu ayun) dan Roller Coaster (kereta luncur). Gerak melingkar vertikal juga dialami oleh seseorang yang mengendarai mobil di daerah perbukitan yang naik turun atau pilot yang melakukan demonstrasi gerakan loop di langit.

Pada kesempatan kali ini, kita akan belajar mengenai cara menentukan rumus gaya tegangan tali pada benda yang bergerak melingkar vertikal. Misalnya, sebuah batu yang diikat dengan seutas tali kemudian diputar secara vertikal. Jika kalian pernah melakukannya, tentu kalian akan merasakan perbedaan tegangan tali saat benda berada di titik tertinggi, terendah, mendatar dan sembarang titik yang membentuk sudut θ.

Pada saat benda berada di titik terendah, Tegangan tali yang kita rasakan cukup besar. Namun seiring benda bergerak melingkar ke atas, tegangan tali yang kita rasakan semakin lama semakin kecil dan puncaknya, ketika benda mencapai titik tertinggi, tegangan tali hampir tidak kita rasakan sama sekali. Kenapa hal tersebut bisa terjadi? Untuk mengetahui jawabannya, perhatikan penjelasan berikut ini.

Ketika sebuah benda bermassa m diikatkan pada ujung seutas tali kemudian ujung tali lainnya diputar secara vertikal, maka benda tersebut akan bergerak melingkar mengikuti lintasan yang dibentuk putaran tali. Ketika benda bergerak melingkar vertikal, besar gaya tegangan tali di setiap titik sepanjang lintasan berbeda-beda. Perbedaan ini timbul karena terjadinya perubahan arah gaya tegangan tali dan gaya berat benda pada saat tali dan benda berputar.

Coba kalian perhatikan gambar di atas. Di titik A, B, C, D dan E arah gaya tegangan tali T dan gaya berat w terhadap pusat lingkaran berubah-ubah. Di titik A atau titik terendah, tegangan tali dan gaya berat bekerja dalam satu garis tetapi berlawanan arah. Sedangkan di titik E atau titik tertinggi kedua gaya tersebut bekerja searah. Berikut ini akan dibahas rumus gaya tegangan tali di 5 titik tersebut.

#1 Tegangan Tali di Titik Terendah

Perhatikan kembali gambar di atas, di titik A komponen gaya yang bekerja dalam arah radial (berhimpit dengan jari-jari lingkaran) adalah gaya tegangan tali TA dan gaya berat w. Arah gaya tegangan tali menuju pusat lingkaran sedangkan gaya berat menjauhi pusat lingkaran. Dalam gerak melingkar, gaya-gaya yang bekerja dalam arah radial merupakan gaya sentripetal.

Apabila arah gaya menuju pusat lingkaran maka gaya berharga positif. Sedangkan jika menjauhi pusat lingkaran maka gaya berharga negatif. Berdasarkan Hukum II Newton, persamaan gerak benda di titik A adalah sebagai berikut.

ΣFs = mas

TA − w = mas

TA = mas + w

TA = mv2/R + mg

TA = m(v2/R + g)

Karena v2/R = ω2R maka

TA = m(ω2R + g)

Dengan demikian, rumus gaya tegangan tali di titik terendah untuk benda yang bergerak melingkar vertikal adalah sebagai berikut.

TA

=

m(v2/R + g)

TA

=

m(ω2R + g)

Keterangan:
TA	=	Tegangan tali di titik A (N)
m	=	Massa benda (kg)
v	=	Kecepatan linear (m/s)
ω	=	Kecepatan sudut (rad/s)
R	=	Jari-jari lintasan (m)
g	=	Percepatan gravitasi bumi (m/s2)

#2 Tegangan Tali di Titik Bawah Membentuk Sudut

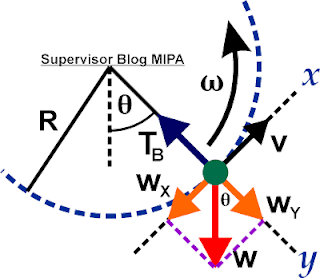
Ketika benda bergerak dari titik terendah (A) menuju titik yang membentuk sudut θ terhadap garis vertikal (B), maka gambar garis-garis gaya yang bekerja pada benda secara detail diperlihatkan seperti pada gambar di bawah ini.

Pertama, gambar gaya tegangan tali yang arahnya sudah pasti menuju pusat lingkaran. Selanjutnya gambar garis gaya berat yang arahnya selalu ke bawah menuju pusat gravitasi bumi. Sekarang coba kalian perhatikan gambar di atas. jika perpanjangan garis gaya tegangan tali dijadikan patokan sumbu-Y dan perpanjangan garis vektor kecepatan linear v dijadikan sebagai sumbu-X, maka gaya berat w membentuk sudut θ terhadap sumbu-Y.

Karena membentuk sudut terhadap sumbu-Y, maka gaya berat w dapat diproyeksikan ke sumbu-X dan juga sumbu-Y sesuai dengan aturan proyeksi vektor. Hasil proyeksi gaya berat ini adalah wX dan wY. Apabila semua gaya telah berhasil digambarkan, maka langkah selanjutnya adalah meninjau gaya-gaya yang bekerja pada arah radial.

Dari gambar di atas, dapat kalian lihat bahwa komponen gaya yang bekerja pada arah radial (berhimpit dengan jari-jari lingkaran) adalah gaya tegangan tali TB dan proyeksi gaya berat pada sumbu-Y yang disimbolkan dengan wY. Arah TB menuju pusat lingkaran sedangkan wY menjauhi pusat lingkaran. Berdasarkan Hukum Newton, persamaan gerak benda di titik B adalah sebagai berikut.

ΣFs = mas

TB – wY = mas

TB = mas + wY
Kemudian kita lihat hubungan antara w dan wY. Dengan menggunakan konsep trigonometri, maka kita peroleh hubungan antara w dan wY sebagai berikut.

Cos θ = wY/w

wY = w cos θ

Dengan demikian, persamaan gaya tegangan tali sebelumnya dapat kita tulis ulang sebagai berikut.

TB = mas + w cos θ

TB = mv2/R + mg cos θ

TB = m(v2/R + g cos θ)

Karena v2/R = ω2R maka

TB = m(ω2R + g cos θ)

Jadi rumus gaya tegangan tali di titik bawah membentuk sudut tertentu untuk benda yang bergerak melingkar vertikal adalah sebagai berikut.

TB

=

m(v2/R + g cos θ)

TB

=

m(ω2R + g cos θ)

Keterangan:
TB	=	Tegangan tali di titik B (N)
m	=	Massa benda (kg)
v	=	Kecepatan linear (m/s)
ω	=	Kecepatan sudut (rad/s)
R	=	Jari-jari lintasan (m)
g	=	Percepatan gravitasi bumi (m/s2)
θ	=	Sudut antara tali dan garis vertikal

#3 Tegangan Tali di Titik Tengah

Coba kalian amati lagi gambar pertama. Ketika benda berada di titik C atau titik tengah, maka benda dikatakan berada pada posisi seimbang. Di titik ini, komponen gaya yang bekerja dalam arah radial hanya gaya tegangan tali sedangkan gaya berat bekerja tegak lurus terhadap arah radial. Dengan demikian, yang berperan sebagai gaya sentripetal adalah gaya tegangan tali saja. Menurut Hukum II Newton, persamaan gerak benda di titik C adalah sebagai berikut.

ΣFs = mas

TC = mas

TC = mv2/R

Karena v2/R = ω2R maka

TC = mω2R

Dengan demikian, rumus gaya tegangan tali di titik tengah untuk benda yang bergerak melingkar vertikal adalah sebagai berikut.

TC

=

mv2/R

TC

=

mω2R

Keterangan:
TC	=	Tegangan tali di titik C (N)
m	=	Massa benda (kg)
v	=	Kecepatan linear (m/s)
ω	=	Kecepatan sudut (rad/s)
R	=	Jari-jari lintasan (m)
g	=	Percepatan gravitasi bumi (m/s2)

#4 Tegangan Tali di Titik Atas Membentuk Sudut

Ketika benda mencapai titik D yang membentuk sudut sebesar θ terhadap garis vertikal, maka arah gaya tegangan tali menuju pusat lingkaran sedangkan arah gaya berat lurus ke bawah menuju pusat bumi. Seperti pada pembahasan sebelumnya, ketika benda berada di titik dengan sudut kemiringan tertentu, maka gaya beratnya dapat diproyeksikan terhadap sumbu-X dan sumbu-Y. Perhatikan gambar berikut.

Coba kalian amati gambar di atas secara cermat. Apabila perpanjangan garis gaya tegangan tali dijadikan sebagai sumbu-Y dan perpanjangan garis vektor kecepatan linear v dijadikan sebagai sumbu-X, maka gaya berat akan membentuk sudut θ terhadap sumbu-Y. Dengan demikian, gaya berat dapat diproyeksikan pada sumbu-X dan sumbu-Y.

Apabila proyeksi gaya berat w terhadap sumbu-X dilambangkan dengan wX dan proyeksi gaya berat w terhadap sumbu-Y dilambangkan dengan wY, maka komponen gaya yang bekerja pada arah radial adalah gaya tegangan tali TD dan proyeksi gaya berat pada sumbu-Y atau wY di mana kedua gaya ini arahnya sama-sama menuju pusat lingkaran. Berdasarkan Hukum II Newton, persamaan gerak benda pada titik ini adalah sebagai berikut.

ΣFs = mas

TD + wY = mas

TD + wY = mv2/R

TD = mv2/R – wY

Karena wY = w cos θ maka

TD = mv2/R – w cos θ

TD = mv2/R – mg cos θ

TD = m(v2/R – g cos θ)

Karena v2/R = ω2R maka persamaan di atas dapat kita tulis menjadi

TD = m(ω2R – g cos θ)

Dengan demikian, rumus gaya tegangan tali di titik atas membentuk sudut tertentu untuk benda yang bergerak melingkar vertikal adalah sebagai berikut.

TD

=

m(v2/R − g cos θ)

TD

=

m(ω2R − g cos θ)

Keterangan:
TD	=	Tegangan tali di titik D (N)
m	=	Massa benda (kg)
v	=	Kecepatan linear (m/s)
ω	=	Kecepatan sudut (rad/s)
R	=	Jari-jari lintasan (m)
g	=	Percepatan gravitasi bumi (m/s2)
θ	=	Sudut antara tali dan garis vertikal

#4 Tegangan Tali di Titik Tertinggi

Sekali lagi, coba kalian perhatikan gambar pertama di atas. Di titik E atau titik tertinggi arah gaya tegangan tali dan gaya berat sama-sama menuju pusat lingkaran sehingga kedua gaya ini berperan sebagai gaya sentripetal positif. Berdasarkan Hukum II Newton, persamaan gerak benda di titik teratas adalah sebagai berikut.

ΣFs = mas

TE + w = mas

TE = mas − w

TE = mv2/R − mg

TE = m(v2/R − g)

Karena v2/R = ω2R maka

TE = m(ω2R − g)

Dengan demikian, rumus gaya tegangan tali di titik terendah untuk benda yang bergerak melingkar vertikal adalah sebagai berikut.

TE

=

m(v2/R − g)

TE

=

m(ω2R − g)

Keterangan:
TE	=	Tegangan tali di titik E (N)
m	=	Massa benda (kg)
v	=	Kecepatan linear (m/s)
ω	=	Kecepatan sudut (rad/s)
R	=	Jari-jari lintasan (m)
g	=	Percepatan gravitasi bumi (m/s2)

Dari penjelasan di atas, kita peroleh rumus besar gaya tegangan tali di titik terendah adalah T = mas + w sedangkan di titik tertinggi besar gaya tegangan talinya adalah T = mas – w. Dengan demikian, di titik terendah T merupakan gaya tegangan tali maksimum karena berfungsi untuk mengimbangi gaya berat benda agar benda tidak jatuh ke bawah dan tetap bergerak melingkar.

Sedangkan di titik tertinggi, nilai T merupakan nilai minimum karena arah gaya berat searah dengan gaya tegangan tali sehingga gaya tegangan tali tidak berfungsi untuk melawan gaya berat. Itulah kenapa pada saat di titik terendah, tegangan tali yang kita rasakan cukup besar sedangkan di titik tertinggi kita hampir tidak merasakan tegangan tali.

Contoh Soal #1

Nizar mengikat bolpointnya yang bermassa 0,1 kg dengan seutas tali dan diputar vertikal dengan kecepatan tetap 4 m/s. Jika panjang tali 1 m dan percepatan gravitasi bumi 10 m/s2, maka tentukan tegangan tali saat bolpoint berada di posisi terendah dan posisi tertinggi!

Jawab

Diketahui:

m = 0,1 kg

v = 4 m/s

r = 1 m

g = 10 m/s2

maka gaya tegangan tali di titik terendah adalah

TA = m(v2/R + g)

TA = (0,1)[(4)2/1 + 10]

TA = (0,1)(16 + 10)

TA = (0,1)(26)

TA = 2,6 N

Sedangkan gaya tegangan tali di titik tertinggi adalah

TA = m(v2/R − g)

TA = (0,1)[(4)2/1 − 10]

TA = (0,1)(16 − 10)

TA = (0,1)(6)

TA = 0,6 N

Contoh Soal #2

Sebuah benda bermassa 2 kg diikat dengan seutas tali yang memiliki panjang 1,5 meter. Kemudian, benda tersebut diputar menurut lintasan lingkaran vertikal dengan kecepatan sudut tetap. Jika g = 10 m/s2 dan pada saat benda di titik terendah, tali mengalami tegangan sebesar 47 Newton, kecepatan sudutnya (dalam rad/s) adalah

Jawab

Diketahui:

TA = 47

m = 2 kg

r = 1,5 m

g = 10 m/s2

Rumus gaya tegangan tali di titik terendah adalah

TA = mω2R + mg

mω2R = TA – mg

ω2 = (TA – mg)/mR

ω = √[(TA – mg)/mR]

ω = √[(47 – 2×10)/(2)(1,5)]

ω = √[(47 – 20)/3]

ω = √(27/3)

ω = √9

ω = 3 rad/s

Demikianlah artikel tentang rumus gaya tegangan tali pada gerak melingkar vertikal beserta gambar ilustrasi dan diagram gayanya dilengkapi contoh soal dan pembahasan. Semoga dapat bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, huruf, ataupun angka dalam perhitungan, mohon informasikan kepada kami via Contact Us. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.