Hukum Newton Pada Gerak Benda yang Dihubungkan Katrol di Bidang Datar dan Miring

Daftar Materi Fisika

• 1. Besaran Fisika
• 2. Vektor dan Resultan
• 3. Mekanika (Kinematika dan Dinamika)
• 4. Fisika Optik
• 5. Suhu dan Kalor

Advertisement

Baca Juga:

Model sistem katrol untuk materi dinamika translasi yang akan kita pelajari kali ini adalah tentang gerak dua benda yang dihubungkan seutas tali melalui sebuah katrol dimana salah satu benda terletak pada bidang datar dan benda lainnya terletak di bidang miring dengan sudut kemiringan tertentu. Keadaan bidang datar atau bidang miring yang akan dibahas dalam artikel ini adalah licin dan juga kasar. Untuk memahaminya, silahkan kalian simak penjelasan berikut ini.

#1 Bidang Datar dan Bidang Miring Licin

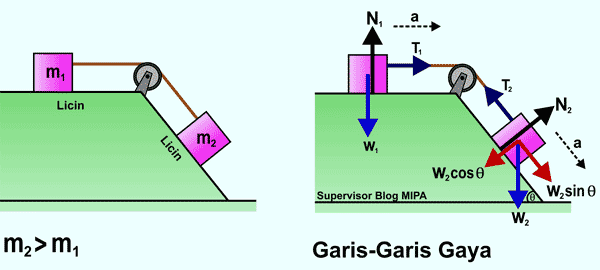
Dua benda anggaplah balok 1 dan 2 bermassa m1 dan m2 dihubungkan dengan seutas tali melalui sebuah katrol yang licin dan massa diabaikan. Balok 1 terletak di bidang datar licin dan balok 2 terletak di bidang miring licin dengan sudut kemiringan bidang sebesar θ. Apabila massa balok 2 lebih besar dari balok 1 (m2 > m1), maka balok 1 akan bergerak ke kanan dan balok 2 akan bergerak ke bawah sejajar bidang miring dengan percepatan a.

Garis-garis gaya yang bekerja pada masing-masing benda diperlihatkan seperti pada gambar di atas. Karena benda 2 terletak pada bidang miring yang memiliki sudut kemiringan sebesar θ, maka gaya berat balok 2 memiliki dua komponen yaitu w2 sin θ dan w2 cos θ. Untuk benda 1 yang bergerak ke kanan, maka perpindahan juga ke arah kanan sehingga gaya-gaya yang arahnya ke kanan berharga positif.

Sementara untuk benda 2 yang bergerak ke bawah sejajar bidang, maka perpindahan benda juga ke arah bawah sehingga gaya-gaya yang arahnya ke bawah sejajar bidang berharga positif dan yang ke atas berharga negatif. Dengan demikian, resultan gaya-gaya yang bekerja pada benda 1 dan benda 2 berdasarkan Hukum Newton adalah sebagai berikut.

Resultan Gaya yang Bekerja pada Balok 1

ΣF1 = m1a

T1 = m1a ..………………….. Pers. (1)

Resultan Gaya yang Bekerja pada Balok 2

ΣF2 = m2a

w2 sin θ – T2 = m2a

m2g sin θ – T2 = m2a …... Pers. (2)

Karena massa katrol dan gesekan pada katrol diabaikan, maka selama sistem bergerak besarnya gaya tegangan tali pada kedua ujung tali adalah sama yaitu T1 = T2. Dengan demikian, apabila kita subtitusikan persamaan (1) ke persamaan (2) kita peroleh persamaan berikut.

m2g sin θ – T2 = m2a

m2g sin θ – m1a = m2a

m2a + m1a = m2g sin θ

m2a + m1a = m2g sin θ

(m2 + m1)a = m2g sin θ

a = m2g sin θ/(m2 + m1) …... Pers. (3)

Dengan demikian, rumus percepatan pada gerak benda-benda yang dihubungkan tali melalui sebuah katrol di mana salah satu benda terletak di bidang datar licin dan benda lainnya terletak di bidang miring licin adalah sebagai berikut.

a	=	m2g sin θ
		m1 + m2

Jika rumus percepatan gerak benda sudah diketahui, maka kita dapat menentukan besar gaya tegangan tali yang bekerja pada kedua balok di atas, yaitu dengan mensubtitusikan rumus percepatan pada persamaan (3) ke persamaan (1). Perhatikan perhitungan berikut ini.

T1 = m1a

T1 = m1{ m2g sin θ/(m2 + m1)}

T1 = m1m2g sin θ/(m2 + m1) …... Pers. (4)

Jadi, besarnya gaya tegangan tali yang bekerja pada kedua balok dapat kita hitungan dengan menggunakan rumus berikut ini.

T1	=	T2	=	m1m2g sin θ
				m1 + m2

Keterangan:
w	=	Gaya berat (N)
T1	=	Gaya tegangan tali pada benda 1 (N)
T2	=	Gaya tegangan tali pada benda 2 (N)
m1	=	Massa benda 1 (kg)
m2	=	Massa benda 2 (kg)
θ	=	Sudut kemiringan bidang miring
a	=	Percepatan benda (m/s2)
g	=	Percepatan gravitasi bumi (m/s2)

#2 Bidang Datar dan Bidang Miring Kasar

Sekarang kita akan membahas kondisi bidang datar dan bidang miring kasar. Karen bidang kasar, tentu kita akan memperhitungkan keberadaan gaya gesek yang bekerja antara permukaan benda terhadap bidang. Tentunya kalian telah mengetahui bahwa besarnya gaya gesek dipengaruhi oleh gaya normal di mana gaya normal ini bekerja dalam arah sumbu-Y. Oleh karena itu, selain resultan gaya yang bekerja pada sumbu-X, kita juga akan menguraikan resultan gaya pada sumbu-Y untuk masing-masing benda.

Jika massa benda 2 lebih besar dari massa benda 1 (m2 > m1), besar koefisien gesek antara benda 1 dengan permukaan bidang datar adalah μ1, koefisien gesek benda 2 dengan bidang miring adalah μ2 sementara itu, benda 2 bergerak ke bawah sejajar bidang dan benda 1 bergerak ke kanan dengan percepatan yang sama sebesar a, maka persamaan gerak masing-masing benda menurut Hukum Newton adalah sebagai berikut.

Resultan Gaya yang Bekerja pada Balok 1

ΣF1Y = m1a

N1 – w1 = m1a

N1 – m1g = m1a

Karena tidak terjadi gerak dalam arah sumbu-Y, maka a = 0 sehinga

N1 – m1g = 0

N1 = m1g .……………..…….. Pers. (5)

ΣF1X = m1a

T1 – f1 = m1a

T1 – μ1N1 = m1a

Karena N1 = m1g maka

T1 – μ1m1g = m1a

T1 = m1a + μ1m1g .……..….. Pers. (6)

Resultan Gaya yang Bekerja pada Balok 2

ΣF2Y = m2a

N2 – w2 cos θ = m2a

N2 – m2g cos θ = m2a

Karena tidak terjadi gerak dalam arah sumbu-Y, maka a = 0 sehinga

N2 – m2g cos θ = 0

N2 = m2g cos θ ……..…….. Pers. (7)

ΣF2X = m2a

w2 sin θ – T2 – f2 = m2a

w2 sin θ – T2 – μ2N2 = m2a

m2g sin θ – T2 – μ2N2 = m2a

Karena N2 = m2g cos θ maka

m2g sin θ – T2 – μ2m2g cos θ = m2a .……..….. Pers. (8)

karena T2 = T1 maka apabila kita subtitusikan persamaan (6) ke persamaan (8) kita peroleh

m2g sin θ – T2 – μ2m2g cos θ = m2a

m2g sin θ – (m1a + μ1m1g)  – μ2m2g cos θ = m2a

m2g sin θ – m1a – μ1m1g  – μ2m2g cos θ = m2a

m2a + m1a = m2g sin θ – μ2m2g cos θ – μ1m1g 

(m2 + m1)a = (m2 sin θ – μ2m2 cos θ – μ1m1)g

a = (m2 sin θ – μ2m2 cos θ – μ1m1)g/(m2 + m1) .……..….. Pers. (9)

Dengan demikian, besar percepatan pada gerak benda-benda yang dihubungkan tali melalui sebuah katrol di mana salah satu benda terletak di bidang datar kasar dan benda lainnya terletak di bidang miring kasar, dapat dihitung dengan rumus berikut.

a	=	(m2 sin θ – μ2m2 cos θ – μ1m1)g
		m1 + m2

Besarnya gaya tegangan tali untuk kondisi bidang datar dan bidang miring kasar dapat ditentukan dengan mensubtitusikan persamaan (9) ke persamaan (6) sebagai berikut.

T1 = m1a + μ1m1g

T1 = m1{(m2 sin θ – μ2m2 cos θ – μ1m1)g/(m2 + m1)} + μ1m1g

T1 = {(m1m2g sin θ – μ2m1m2g cos θ – μ1m12g)/(m2 + m1)} + μ1m1g

T1 = (m1m2g sin θ – μ2m1m2g cos θ – μ1m12g + μ1m1m2g + μ1m12g)/(m2 + m1)

T1 = (m1m2g sin θ – μ2m1m2g cos θ + μ1m1m2g)/(m2 + m1)

T1 = {m1m2g(sin θ – μ2 cos θ + μ1)}/(m2 + m1) .……..….. Pers. (10)

Jadi, besarnya gaya tegangan tali yang bekerja pada kedua balok pada kondisi bidang datar dan bidang miring kasar, dapat kita tentukan dengan menggunakan rumus sebagai berikut.

T1	=	T2	=	(sin θ – μ2 cos θ + μ1)m1m2g
				m1 + m2

Keterangan:
w	=	Gaya berat (N)
N	=	Gaya normal (N)
f1	=	Gaya gesek benda 1 terhadap bidang datar (N)
f2	=	Gaya gesek benda 2 terhadap bidang miring (N)
T1	=	Gaya tegangan tali pada benda 1 (N)
T2	=	Gaya tegangan tali pada benda 2 (N)
μ1	=	Koefisien gesek benda 1 terhadap bidang datar
μ1	=	Koefisien gesek benda 2 terhadap bidang miring
m1	=	Massa benda 1 (kg)
m2	=	Massa benda 2 (kg)
θ	=	Sudut kemiringan bidang miring
a	=	Percepatan benda (m/s2)
g	=	Percepatan gravitasi bumi (m/s2)

Demikianlah artikel tentang penerapan Hukum Newton pada gerak dua benda yang dihubungkan tali melalui sebuah katrol di bidang datar dan bidang miring baik licin ataupun kasar lengkap dengan gambar ilustrasi dan garis-garis gayanya. Semoga dapat bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, huruf maupun angka dalam perhitungan mohon dimaklumi. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.