Hukum Newton Pada Gerak Benda di Bidang Miring Licin
https://www.fisikabc.com/2017/07/gerak-benda-pada-bidang-miring-licin.html?m=0
Daftar Materi Fisika
Advertisement
Baca Juga:
Pada kesempatan kali ini, penulis akan mengulas secara detail mengenai penerapan hukum Newton pada bidang miring khususnya bidang miring licin dimana tidak ada gesekan antara permukaan benda dengan permukaan bidang. Penerapan hukum Newton pada bidang miring licin sedikit berbeda dengan penerapan hukum Newton pada gerak benda di bidang datar licin karena gaya berat pada bidang miring memiliki komponen pada sumbu-X dan sumbu-Y.
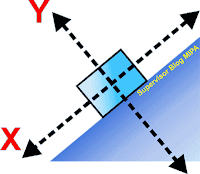
Sebelum membahas gerak benda di bidang miring licin, kalian harus tahu lebih dahulu mana yang menjadi acuan sumbu-X dan sumbu-Y. Untuk itu, perhatikan gambar berikut ini.
Dari gambar di atas, yang menjadi patokan sumbu-X adalah garis yang sejajar bidang miring, sehingga gaya-gaya yang bekerja pada arah ini merupakan gaya pada sumbu-X (FX) sedangkan sumbu-Y adalah garis yang tegak lurus dengan bidang miring sehingga gaya pada arah ini disebut gaya pada sumbu-Y (FY). Kita akan membahas aplikasi hukum Newton pada gerak benda di bidang miring licin dalam 5 kondisi, yaitu
1.Benda pada bidang miring licin tanpa gaya luar
2.Benda ditarik atau didorong sejajar bidang miring
3.Benda ditekan pada bidang miring licin
4.Benda didorong horizontal
5.Benda ditarik vertikal
Dari lima kondisi tersebut, yang sering muncul dalam soal fisika tentang dinamika adalah kondisi 1 dan 2, akan tetapi hanya sekedar menambah wawasan kalian saja maka penulis merasa perlu untuk mengulas tiga kondisi lainnya. Untuk itu, silakan kalian simak baik-baik penjelasan berikut ini.
#1 Benda pada Bidang Miring Licin Tanpa Gaya Luar
Sebuah benda terletak pada bidang miring licin tanpa gaya luar diperlihatkan pada gambar di atas. Gaya-gaya yang bekerja adalah gaya normal N dan gaya berat w. Karena bentuk bidang adalah miring, maka gaya berat w memiliki komponen pada sumbu-X dan sumbu-Y yaitu w sin α dan w cos α. Dari gambar garis-garis gaya di atas, gaya yang bekerja pada sumbu-X hanyalah w sin α sehingga benda akan bergerak ke bawah. Dalam hal ini berlaku Hukum Newton sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – w cos α = 0
N = w cos α
Dengan demikian besar gaya normal akan sama dengan komponen gaya berat benda pada sumbu-Y, sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = mg cos α
|
Resultan gaya pada sumbu-X
ΣFX = ma
w sin α = ma
mg sin α = ma
a = g sin α
Dengan demikian, rumus percepatan benda yang bergerak pada bidang miring licin tanpa gaya luar adalah sebagai berikut.
a = g sin α
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#2 Benda Ditarik atau Didorong Sejajar Bidang Miring
Ketika sebuah benda yang terletak pada bidang miring didorong atau ditarik sejajar bidang tentu saja memiliki konsep yang sama yaitu menghasilkan gaya F ke atas seperti yang diperlihatkan pada gambar di atas. Pada keadaan ini, ada tiga kemungkinan gerak benda yaitu benda diam, benda bergerak ke atas atau benda bergerak ke bawah.
Benda diam
Benda diam hanya terjadi jika F = w sin α, persamaan hukum Newton pada keadaan ini adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – w cos α = 0
N = w cos α
Dengan demikian persamaan gaya normal pada benda yang didorong atau ditarik sejajar bidang miring adalah sebagai berikut.
N = mg cos α
|
Persamaan gaya normal pada kemungkinan pertama ini juga berlaku pada dua kemungkinan yang lain sehingga pada dua kemungkinan tersebut tidak perlu diuraikan lagi.
Resultan gaya pada sumbu-X
ΣFX = ma
F – w sin α = ma
Karena benda dalam keadaan diam, maka a = 0 sehingga
F – w sin α = 0
F = w sin α
Sehingga persamaan gerak benda yang diam setelah diberi gaya tarik atau dorong sejajar bidang miring licin adalah sebagai berikut.
F = mg sin α
|
Benda bergerak ke atas
Benda bergerak ke atas dapat terjadi jika F > w sin α. Resultan gaya pada sumbu-X yang bekerja pada benda adalah sebagai berikut.
ΣFX = ma
F – w sin α = ma
F = ma + w sin α
F = ma + mg sin α
F = m(a + g sin α)
Dengan demikian persamaan gerak pada benda yang bergerak ke atas di bidang miring licin setelah mendapat gaya tarik atau dorong sejajar bidang adalah sebagai berikut.
F = m(a + g sin α)
|
Benda bergerak ke bawah
Benda bergerak ke bawah dapat terjadi jika F < w sin α. Resultan gaya pada sumbu-X yang bekerja pada benda adalah sebagai berikut.
ΣFX = ma
w sin α – F = ma
F = w sin α – ma
F = mg sin α – ma
F = m(g sin α – a)
Dengan demikian persamaan gerak pada benda yang bergerak ke bawah di bidang miring licin setelah mendapat gaya tarik atau dorong sejajar bidang adalah sebagai berikut.
F = m(g sin α – a)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tarik atau dorong (N)
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#3 Benda Ditekan pada Bidang Miring Licin
Sebuah benda yang terletak pada bidang miring licin ditekan dengan gaya yang tegak lurus dengan bidang seperti yang ditunjukkan pada gambar di atas. Jika kalian perhatikan gambar garis-garis gaya di atas, gaya yang bekerja pada sumbu-X hanya w sin α sehingga benda tetap akan bergerak ke bawah. Hukum Newton pada keadaan ini adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – F – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – F – w cos α = 0
N = F + w cos α
Dengan demikian besar gaya normal akan sama dengan komponen gaya berat benda pada sumbu-Y ditambah gaya tekan, sehingga persamaannya dapat kita tuliskan sebagai berikut.
N = F + mg cos α
|
Resultan gaya pada sumbu-X
ΣFX = ma
w sin α = ma
mg sin α = ma
a = g sin α
Dengan demikian, rumus percepatan benda yang bergerak pada bidang miring licin yang ditekan dengan gaya F adalah sebagai berikut.
a = g sin α
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tekan
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#4 Benda Didorong Horizontal pada Bidang Miring Licin
Sebuah benda pada bidang miring licin diberi gaya dorong horizontal seperti yang ditampilkan pada gambar di atas. Gaya dorong F tidak sejajar dengan sumbu-X maupun sumbu-Y sehingga gaya F dapat diuraikan pada sumbu-X dan Y sama seperti gaya berat w. komponen gaya F pada sumbu-X dan sumbu-Y adalah F cos α dan F sin α. Pada kondisi ini ada tiga kemungkinan gerak benda yaitu benda diam, benda bergerak ke atas atau benda bergerak ke bawah.
Benda diam
Benda diam hanya terjadi jika F cos α = w sin α, persamaan hukum Newton pada keadaan ini adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – F sin α – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – F sin α – w cos α = 0
N = F sin α + w cos α
Dengan demikian rumus gaya normal pada benda yang didorong horizontal pada bidang miring licin adalah sebagai berikut.
N = F sin α + mg cos α
|
Rumus gaya normal tersebut juga berlaku untuk kemungkinan benda bergerak ke atas maupun bergerak ke bawah.
Resultan gaya pada sumbu-X
ΣFX = ma
F cos α – w sin α = ma
Karena benda dalam keadaan diam, maka a = 0 sehingga
F cos α – w sin α = 0
F cos α = w sin α
F = w sin α/cos α
F = w tan α
Sehingga persamaan gerak benda yang diam setelah diberi gaya dorong horizontal pada bidang miring licin adalah sebagai berikut.
F = mg tan α
|
Benda bergerak ke atas
Benda bergerak ke atas dapat terjadi jika F cos α > w sin α. Resultan gaya pada sumbu-X yang bekerja pada benda adalah sebagai berikut.
ΣFX = ma
F cos α – w sin α = ma
F cos α = ma + w sin α
F cos α = ma + mg sin α
F = (ma + mg sin α)/cos α
F = ma sec α + mg tan α
F = m(a sec α + g tan α)
Dengan demikian persamaan gerak pada benda yang bergerak ke atas di bidang miring licin setelah diberi gaya dorong horizontal adalah sebagai berikut.
F = m(a sec α + g tan α)
|
Benda bergerak ke bawah
Benda bergerak ke bawah dapat terjadi jika F cos α < w sin α. Resultan gaya pada sumbu-X yang bekerja pada benda adalah sebagai berikut.
ΣFX = ma
w sin α – F cos α = ma
F cos α = w sin α – ma
F cos α = mg sin α – ma
F = (mg sin α – ma)/cos α
F = mg tan α – ma sec α
F = m(g tan α – a sec α)
Dengan demikian persamaan gerak pada benda yang bergerak ke bawah di bidang miring licin setelah mendapat gaya dorong horizontal adalah sebagai berikut.
F = m(g tan α – a sec α)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya dorong horizontal (N)
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#5 Benda Ditarik Vertikal pada Bidang Miring Licin
Sebuah benda yang berada di atas bidang miring licin kemudian ditarik vertikal diperlihatkan pada gambar di atas. Jika kalian perhatikan gambar garis-garis gaya yang bekerja pada benda, gaya F sejajar dengan gaya berat w, sehingga gaya F ini juga memiliki komponen pada sumbu-X dan sumbu-Y yaitu F sin α dan F cos α. Pada kondisi benda seperti ini, ada tiga kemungkinan gerak benda, yaitu benda diam, benda bergerak vertikal ke atas atau benda bergerak ke bawah.
Benda diam
Benda diam hanya terjadi jika F = w, persamaan hukum Newton pada keadaan ini adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N + F cos α – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N + F cos α – w cos α = 0
N = w cos α – F cos α
Dengan demikian persamaan gaya normal pada benda yang ditarik vertikal pada bidang miring licin adalah sebagai berikut.
N = mg cos α – F cos α
|
Rumus gaya normal tersebut juga berlaku untuk kemungkinan benda bergerak ke bawah.
Resultan gaya pada sumbu-X
ΣFX = ma
F sin α – w sin α = ma
Karena benda diam, maka a = 0 sehingga
F sin α – w sin α = 0
F sin α = w sin α
F = w
F = mg
Sehingga persamaan gerak benda yang diam setelah diberi gaya tarik vertikal pada bidang miring licin adalah sebagai berikut.
F = mg
|
Benda bergerak vertikal ke atas
Benda bergerak vertikal ke atas dapat terjadi jika F > w. Karena benda bergerak vertikal ke atas, maka benda tidak lagi menyentuh bidang miring sehingga gaya normal akan hilang dengan kata lain gaya yang bekerja pada benda hanya gaya tarik F dan gaya berat w. Oleh karena benda tidak menyentuh bidang, maka hukum Newton pada bidang miring tidak berlaku, sehingga kita tidak perlu membahas kondisi ini lebih jauh lagi.
Benda bergerak ke bawah
Benda bergerak ke bawah dapat terjadi jika F < w. Resultan gaya pada sumbu-X yang bekerja pada benda adalah sebagai berikut.
ΣFX = ma
w sin α – F sin α = ma
F sin α = w sin α – ma
F sin α = mg sin α – ma
F = (mg sin α – ma)/sin α
F = mg – ma cosec α
F = m(g – a cosec α)
Dengan demikian persamaan gerak pada benda yang bergerak ke bawah di bidang miring licin setelah mendapat gaya tarik vertikal adalah sebagai berikut.
F = m(g – a cosec α)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tarik vertikal (N)
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
Demikianlah artikel tentang penerapan atau aplikasi Hukum Newton pada gerak benda di bidang miring licin beserta gambar dan penjelasannya. Untuk penerapan Hukum Newton pada bidang miring kasar silahkan kalian simak artikel tentang hukum Newton pada gerak benda di bidang miring kasar. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di atikel berikutnya.





Kak mau nanya . . .
ReplyDeleteApakah rumus-rumus diatas bisa digunakan untuk menyelesaikan bidang miring yg menggunakan katrol ???
Nggk bisa dong, untuk bidang miring menggunakan katrol silahkan kamu pelajari materi ini:
DeleteHukum Newton pada Gerak Benda yang Dihubungkan Katrol di Bidang Miring
Kak gimana kalo bidang miring yg juga diketahui jaraknya , rumus nya yaapa? :)
ReplyDeleteKlo udah pake jarak berarti itu udah masuk ke materi usaha dan energi
Deletebgmna menghitung percepatan benda dan kecepatan benda pada bidang miring licin? jika hnya diketauhi sudutnya dan massanya.
ReplyDeletebgmna mengghitung a dan v jika yng diketahui hnya massa dan sudutnya?
ReplyDeleteIni untuk kondisi benda bergerak di bidang miring ya?
DeleteSoal lengkapnya ada tidak?
Kalau benda makin berat, apakah percepatan juga makin besar ?
ReplyDeleteBagaiman menghitung kecepatan pada titik "n" ?
rumus percepatan adalah sebgai berikut
Deletea = g sin α
jadi cuman dipengaruhi oleh percepatan gravitasi bumi dan kemiringan sudut bidang, dengan kata lain berat benda tidak berpengaruh thdp seberapa besar percepatannya benda tsb.
Bagaimana cara menentukan percepatan gerak sistem jika permukaan yang bersentuhan dengan balok licin, yang diketahui hanya massa dan sudut apit saja.Tidak ada tegangan tali
ReplyDelete