Hukum Newton Pada Gerak Benda di Bidang Miring Kasar 3
https://www.fisikabc.com/2017/07/gerak-benda-pada-bidang-miring-kasar-3.html?m=0
Daftar Materi Fisika
Advertisement
Baca Juga:
Artikel ini merupakan sesi terakhir dari kelanjutan artikel tentang penerapan hukum Newton pada gerak benda di bidang miring kasar bagian 1 dan bagian 2. Untuk menyelesaikan permasalahan yang berhubungan dengan gerak benda pada bidang miring kasar, ada beberapa catatan penting yang perlu kalian perhatikan, yaitu.
■ Pertama, gambarlah diagram secara terpisah yang menggambarkan semua gaya yang bekerja pada benda (gambar diagram bebas).
■ Kedua, gaya yang searah dengan perpindahan benda dianggap positif, sedangkan gaya yang berlawanan arah dengan perpindahan benda dianggap negatif.
■ Ketiga, gaya gesek selalu berlawanan arah dengan perpindahan benda. Pada benda yang diam, bekerja gaya gesek statis (fs) dan pada benda yang bergerak bekerja gaya gesek kinetis (fk).
■ Pertama, gambarlah diagram secara terpisah yang menggambarkan semua gaya yang bekerja pada benda (gambar diagram bebas).
■ Kedua, gaya yang searah dengan perpindahan benda dianggap positif, sedangkan gaya yang berlawanan arah dengan perpindahan benda dianggap negatif.
■ Ketiga, gaya gesek selalu berlawanan arah dengan perpindahan benda. Pada benda yang diam, bekerja gaya gesek statis (fs) dan pada benda yang bergerak bekerja gaya gesek kinetis (fk).
Pada kesempatan kali ini, kita akan mengulas aplikasi hukum Newton pada gerak benda di bidang miring kasar dalam dua kondisi, yaitu benda ditarik secara vertikal dan benda didorong secara vertikal. Untuk memahaminya, silahkan kalian perhatikan penjelasan berikut ini.
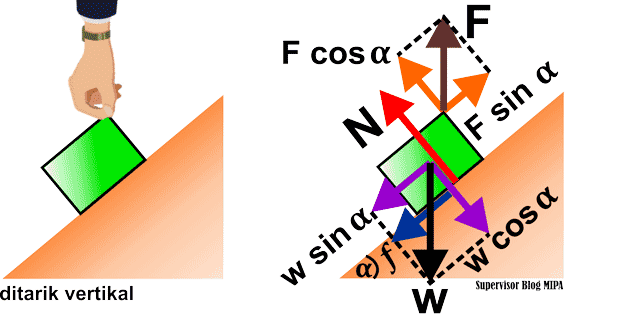
#1 Benda Ditarik Vertikal pada Bidang Miring Kasar
Sebuah benda yang terletak pada bidang miring kasar ditarik secara vertikal, garis-garis gaya yang bekerja pada benda diperlihatkan pada gambar di atas. Jika kita analisis arah gaya-gayanya, maka terdapat 4 kemungkinan gerak benda yaitu benda diam, benda bergerak ke bawah, benda bergerak ke atas atau benda mengalami gerak vertikal ke atas. Namun pada pembahasan ini, kita tidak membicarakan gerak vertikal sebab jika benda bergerak dalam arah vertikal, hukum Newton pada bidang miring tidak berlaku.
Benda Diam
Benda diam dapat terjadi jika F sin α = w sin α + f. Apabila benda diam, gaya gesek yang bekerja pada benda adalah gaya gesek statis (fs). Jika koefisien gesek statis adalah μs maka persamaan gerak benda menurut Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N + F cos α – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N + F cos α – w cos α = 0
N = w cos α – F cos α
Dengan demikian rumus gaya normal pada benda yang diam di bidang miring kasar setelah ditarik vertikal adalah sebagai berikut.
N = mg cos α – F cos α
|
Persamaan gaya normal di atas juga berlaku untuk dua kemungkinan gerak benda lainnya sehingga tidak perlu diuraikan lagi pada benda yang bergerak ke bawah dan ke atas.
Resultan gaya pada sumbu-X
ΣFX = ma
F sin α – w sin α – fs = ma
F sin α – w sin α – μsN = ma
Karena N = mg cos α – F cos α, maka besar gaya geseknya adalah fs = μs (mg cos α – F cos α) sehingga,
F sin α – w sin α – μs (mg cos α – F cos α) = ma
Karena benda diam, maka a = 0
F sin α – w sin α – μs (mg cos α – F cos α) = 0
F sin α – mg sin α – μs mg cos α + μs F cos α = 0
F sin α + μs F cos α = mg sin α + μs mg cos α
F (sin α + μs cos α) = mg (sin α + μs cos α)
F (tan α + μs) = mg (tan α + μs)
Dengan demikian, persamaan gerak pada benda yang diam di atas bidang miring kasar setelah ditarik horizontal adalah sebagai berikut.
F (tan α + μs) = mg (tan α + μs)
|
Benda Bergerak ke Bawah
Apabila F sin α < w sin α + f maka benda akan bergerak ke bawah dan gaya gesek yang bekerja pada benda adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetik antara permukaan benda dengan bidang adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-X
ΣFX = ma
w sin α – F sin α – fk = ma
w sin α – F sin α – μkN= ma
Karena N = mg cos α – F cos α, maka besar gaya geseknya adalah fk = μk (mg cos α – F cos α) sehingga,
w sin α – F sin α – μk (mg cos α – F cos α) = ma
mg sin α – F sin α – μk mg cos α + μk F cos α = ma
mg sin α – μk mg cos α = ma + F sin α – μk F cos α
F sin α – μk F cos α + ma = mg sin α – μk mg cos α
F (sin α – μk cos α) + ma = mg (sin α – μk cos α)
F (tan α – μk) + ma sec α = mg (tan α – μk)
Dengan demikian, persamaan gerak pada benda yang bergerak ke bawah di bidang miring kasar, setelah ditarik vertikal adalah sebagai berikut.
F (tan α – μk) + ma sec α = mg (tan α – μk)
|
Benda Bergerak ke Atas
Apabila F sin α > w sin α + f maka benda akan bergerak ke bawah dan gaya gesek yang bekerja pada benda adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetisnya adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-X
ΣFX = ma
F sin α – w sin α – fk = ma
F sin α – w sin α – μkN= ma
Karena N = mg cos α – F cos α, maka besar gaya geseknya adalah fk = μk (mg cos α – F cos α) sehingga,
F sin α – w sin α – μk (mg cos α – F cos α) = ma
F sin α – mg sin α – μk mg cos α + μk F cos α = ma
F sin α + μk F cos α – ma = mg sin α + μk mg cos α
F (sin α + μk cos α) – ma = mg (sin α + μk cos α)
F (tan α + μk) – ma sec α = mg (tan α + μk)
Dengan demikian, persamaan gerak pada benda yang bergerak ke atas di bidang miring kasar, setelah ditarik vertikal adalah sebagai berikut.
F (tan α + μk) – ma sec α = mg (tan α + μk)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya tarik (N)
|
f
|
=
|
Gaya gesek (N)
|
fs
|
=
|
Gaya gesek statis (N)
|
fk
|
=
|
Gaya gesek kinetis (N)
|
μs
|
=
|
Koefisien gesek statis
|
μk
|
=
|
Koefisien gesek kinetis
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
| |
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
#2 Benda Didorong Vertikal pada Bidang Miring Kasar
Pada benda yang didorong vertikal di bidang miring kasar, garis-garis gaya yang bekerja ditunjukkan pada gambar di atas. Jika bidang miring adalah zat padat, maka ada dua kemungkinan gerak benda, yaitu benda diam atau bergerak ke bawah.
Benda Diam
Benda diam dapat terjadi jika F sin α + w sin α < f. Apabila benda diam, gaya gesek yang bekerja pada benda adalah gaya gesek statis (fs). Jika koefisien gesek statis adalah μs maka persamaan gerak benda menurut Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-Y
ΣFY = ma
N – F cos α – w cos α = ma
karena benda tidak bergerak pada sumbu-Y maka a = 0, sehingga
N – F cos α – w cos α = 0
N = F cos α + w cos α
Dengan demikian rumus gaya normal pada benda yang diam di bidang miring kasar setelah didorong vertikal adalah sebagai berikut.
N = F cos α + mg cos α
|
Persamaan gaya normal di atas juga berlaku pada benda yang bergerak ke bawah.
Resultan gaya pada sumbu-X
ΣFX = ma
F sin α + w sin α – fs = ma
F sin α + w sin α – μsN = ma
Karena N = F cos α + mg cos α, maka besar gaya geseknya adalah fs = μs (F cos α + mg cos α) sehingga,
F sin α + w sin α – μs (F cos α + mg cos α) = ma
Karena benda diam, maka a = 0
F sin α + w sin α – μs (F cos α + mg cos α) = 0
F sin α + mg sin α – μs F cos α – μs mg cos α = 0
F sin α – μs F cos α = μs mg cos α – mg sin α
F (sin α – μs cos α) = mg (μs cos α – sin α)
F (tan α – μs) = mg (μs – tan α)
Dengan demikian, persamaan gerak pada benda yang diam di atas bidang miring kasar setelah didorong vertikal adalah sebagai berikut.
F (tan α – μs) = mg (μs – tan α)
|
Benda Bergerak ke Bawah
Apabila F sin α + w sin α > f maka benda akan bergerak ke bawah dan gaya gesek yang bekerja pada benda adalah gaya gesek kinetis (fk). Jika koefisien gesek kinetik antara permukaan benda dengan bidang adalah μk maka persamaan gerak benda menggunakan Hukum Newton adalah sebagai berikut.
Resultan gaya pada sumbu-X
ΣFX = ma
F sin α + w sin α – fk = ma
F sin α + w sin α – μkN = ma
Karena N = F cos α + mg cos α, maka besar gaya geseknya adalah fk = μk (F cos α + mg cos α) sehingga,
F sin α + w sin α – μk (F cos α + mg cos α) = ma
F sin α + mg sin α – μk F cos α + μk mg cos α = ma
mg sin α + μk mg cos α = ma – F sin α + μk F cos α
μk F cos α – F sin α + ma = mg sin α + μk mg cos α
F (μk cos α – sin α) + ma = mg (sin α + μk cos α)
F (μk – tan α) + ma sec α = mg (tan α + μk)
Dengan demikian, persamaan gerak pada benda yang bergerak ke bawah di bidang miring kasar, setelah didorong vertikal adalah sebagai berikut.
F (μk – tan α) + ma sec α = mg (tan α + μk)
|
Keterangan:
| ||
N
|
=
|
Gaya normal (N)
|
w
|
=
|
Gaya berat (N)
|
F
|
=
|
Gaya dorong (N)
|
f
|
=
|
Gaya gesek (N)
|
fs
|
=
|
Gaya gesek statis (N)
|
fk
|
=
|
Gaya gesek kinetis (N)
|
μs
|
=
|
Koefisien gesek statis
|
μk
|
=
|
Koefisien gesek kinetis
|
m
|
=
|
Massa benda (kg)
|
α
|
=
|
Sudut kemiringan bidang
|
a
|
=
|
Percepatan benda (m/s2)
|
g
|
=
|
Percepatan gravitasi bumi (m/s2)
|
Demikianlah artikel tentang penerapan atau aplikasi Hukum Newton pada gerak benda di bidang miring kasar lengkap beserta gambar ilustrasi dan garis-garis gayanya. Semoga dapat bermanfaat untuk Anda. Apabila terdapat kesalahan tanda, simbol, huruf maupun angka dalam perhitungan mohon dimaklumi. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.