Rumus Hubungan Roda-Roda Pada Gerak Melingkar Beserta Contoh Soal dan Pembahasan
https://www.fisikabc.com/2017/06/hubungan-roda-roda-gerak-melingkar.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Punyakah kalian sepeda ontel di rumah? Jika punya, coba kalian amati sistem gerak pada sepeda ontel tersebut. Bagi yang tidak punya sepeda ontel di rumah, kalian bisa amati gambar sepeda di atas. Sebuah sepeda ontel memiliki 3 komponen gerak utama yang berbentuk bundar yaitu roda, gir depan dan gir belakang. Ketiga komponen gerak tersebut saling berhubungan membentuk sistem dan dinamakan hubungan roda-roda. Lalu bagaimanakah cara kerja sepeda ontel tersebut?
Sepeda ontel akan bergerak maju jika kita genjot pedal ke depan. Genjotan pada pedal sepeda tersebut memutar gir depan. Gir depan dihubungkan dengan gir belakang menggunakan rantai menyebabkan sepeda dapat bergerak. Jika kalian amati lagi gambar di atas, antara gir depan dan gir belakang dihubungkan menggunakan rantai. Sementara itu, gir belakang dan roda belakang mempunyai satu pusat atau berada pada satu as.
Dengan demikian, pada sistem gerak sepeda ontel terdapat dua hubungan yang berbeda. Hubungan pertama adalah antara gir belakang dengan roda yang berada pada satu pusat atau as dan dinamakan hubungan roda-roda sepusat (seporos). Sedangkan hubungan yang kedua adalah antara gir belakang dengan gir depan yang dihubungkan dengan tali (rantai), hubungan ini dinamakan hubungan roda-rada yang dihubungkan dengan sabuk atau rantai.
Selain dua hubungan roda tersebut, terdapat satu hubungan lagi, yaitu hubungan roda-roda yang bersinggungan. Lalu bagaimanakah persamaan matematis dari hubungan roda-roda tersebut? Setiap jenis hubungan memiliki rumus yang berbeda-beda oleh karena itu, untuk memahami persamaan gerak pada hubungan roda-roda dalam gerak melingkar, silahkan kalian simak penjelasan berikut ini.
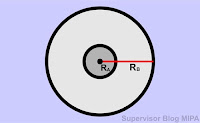
#1 Rumus Hubungan Roda-Roda Sepusat
Gambar di atas adalah contoh ilustrasi hubungan roda-roda satu poros atau satu pusat seperti hubungan roda pada gir belakang dengan roda belakang sepeda ontel. Jadi anggap saja dua lingkaran di atas adalah gir dan roda sepeda. Pada saat sepeda bergerak maju, roda belakang berputar searah jarum jam. Demikian pula dengan gir belakang.
Setelah selang waktu tertentu, gir belakang dan roda menempuh posisi sudut yang sama. Ini berarti, kecepatan sudut gir belakang dan roda belakang adalah sama. Jadi, pada roda-roda yang sepusat berlaku rumus atau persamaan sebagai berikut:
ωA
|
=
|
ωB
| ||||
vA
|
=
|
vB
|
Keterangan:
| |||
RA
|
RB
|
ω
|
=
|
kecepatan sudut (rad/s)
| ||
vA
|
=
|
RA
|
v
|
=
|
kecepatan linear (m/s)
| |
vB
|
RB
|
R
|
=
|
jari-jari (m)
| ||
Contoh Soal 1
Dua buah roda A dan B yang berada pada satu poros memiliki jari-jari 2 cm dan 8 cm, seperti yang terlihat pada gambar dibawah ini. Jika kecepatan linear roda A adalah 6 m/s, tentukan:
a) kecepatan sudut roda A
b) kecepatan linear dan kecepatan sudut roda B
Penyelesaian:
RA = 2 cm = 0,02 m
RB = 8 cm = 0,08 m
vA = 6 m/s
Ditanya: ωA, vB dan ωB
a) kecepatan sudut roda A dapat dihitung dengan rumus berikut:
ωA = vA/RA
ωA = 6/0,02
ωA = 300 rad/s
b) roda A dan B adalah roda-roda sepusat, sehingga berlaku persamaan berikut:
ωB = ωA
ωB = 300 rad/s
kecepatan linear dapat dihitung dengan persamaan berikut:
vB = ωB × R (rumus hubungan besaran sudut dengan linear)
vB = 300 × 0,08
vB = 24 m/s
#2 Rumus Hubungan Roda-Roda yang Dihubungkan dengan Rantai
Gambar di atas adalah contoh ilustrasi hubungan roda-roda yang dihubungkan dengan sabuk atau rantai seperti hubungan roda pada gir belakang dengan gir depan sepeda ontel. Jadi anggap saja dua lingkaran di atas adalah gir belakang dan gir depan sepeda. Ketika sepeda bergerak maju, gir depan dan gir belakang akan berputar searah jarum jam. Sehingga dapat dikatakan arah kecepatan sudut kedua gir adalah sama.
Dari pengertian kecepatan linear, kalian tahu bahwa arah kecepatan linear selalu menyinggung lingkaran. Rantai atau tali yang digunakan untuk menghubungkan gir belakang dan gir depan, dipasang pada sebelah luar setiap gir. Pada saat bergerak, kecepatan rantai atau tali menyinggung bagian luar gir. Sehingga dapat disimpulkan bahwa arah dan besar kecepatan linear (tangensial) pada dua roda yang dihubungkan dengan tali atau rantai adalah sama. Sehingga berlaku persamaan sebagai berikut:
vA
|
=
|
vB
|
Keterangan:
| |||
ωARA
|
=
|
ωBRB
|
ω
|
=
|
kecepatan sudut (rad/s)
| |
v
|
=
|
kecepatan linear (m/s)
| ||||
R
|
=
|
jari-jari (m)
| ||||
Contoh Soal 2
Dua buah roda dihubungkan dengan rantai. Roda yang lebih kecil dengan jari-jari 8 cm diputar pada 100 rad/s. Jika jari-jari roda yang lebih besar adalah 15 cm, berapakah kecepatan linear kedua roda tersebut? Dan berapa juga kecepatan sudut roda yang lebih besar?
Penyelesaian
Penyelesaian
R1 = 8 cm = 0,08 m
R2 = 15 cm = 0,15 m
ω1 = 100 rad/s
Ditanya: kecepatan linear roda 1 dan 2
Dua roda yang dihubungkan dengan tali atau sabuk memiliki kecepatan linear yang sama besar. Jadi kecepatan linear kedua roda tersebut adalah v1 = v2
Kecepatan linear roda 1
v1 = ω1 × R1
v1 = 100 × 0,08
v1 = 8 m/s
Kecepatan linear roda 2
v2 = v1
v2 = 8 m/s
Kecepatan sudut roda 2
v2 = ω2 × R2
ω2 = v2/ R2
ω2 = 8/0,15
ω2 = 53,33 rad/s
#3 Rumus Hubungan Roda-Roda yang Bersinggungan
Hubungan roda-roda yang bersinggungan dapat kalian jumpai pada mesin jam analog, dimana mesin jam tersebut menggunakan roda-roda bergerigi yang saling bersinggungan satu sama lain. Jika kalian tidak percaya, silahkan kalian bongkar jam dinding atau jam tangan analog kalian. Gambar di atas adalah contoh ilustrasi dua roda yang bersinggungan.
Jika roda yang lebih besar berputar searah jarum jam, maka roda yang lebih kecil akan berputar berlawanan arah jarum jam sehingga dapat dikatakan arah kecepatan sudut pada dua roda yang bersinggungan adalah berlawanan. Akan tetapi, pada titik persinggungan, besar kecepatan linear kedua roda adalah sama. Sedangkan kecepatan angulernya akan berbeda, bergantung pada jari-jari masing-masing roda atau jumlah gir yang dimilikinya. Jadi pada dua roda yang saling bersinggungan berlaku persamaan berikut:
Jika roda yang lebih besar berputar searah jarum jam, maka roda yang lebih kecil akan berputar berlawanan arah jarum jam sehingga dapat dikatakan arah kecepatan sudut pada dua roda yang bersinggungan adalah berlawanan. Akan tetapi, pada titik persinggungan, besar kecepatan linear kedua roda adalah sama. Sedangkan kecepatan angulernya akan berbeda, bergantung pada jari-jari masing-masing roda atau jumlah gir yang dimilikinya. Jadi pada dua roda yang saling bersinggungan berlaku persamaan berikut:
vA
|
=
|
vB
|
Keterangan:
| |||
ωARA
|
=
|
ωBRB
|
ω
|
=
|
kecepatan sudut (rad/s)
| |
v
|
=
|
kecepatan linear (m/s)
| ||||
R
|
=
|
jari-jari (m)
| ||||
Info Penting
| ||
Kenapa rumus hubungan roda-roda yang bersinggungan sama dengan rumus hubungan roda-roda yang dihubungkan dengan rantai? Sebenarnya, hubungan roda yang dihubungkan dengan rantai itu termasuk hubungan roda yang bersinggungan yang membedakan hanya kontak langsung atau tidak langsung antara roda pertama dengan roda kedua.
Jika hubungan roda-roda yang bersinggungan terjadi kontak langsung antara dua roda maka pada hubungan roda-roda yang dihubungkan dengan tali terjadi kontak tidak langsung antara dua roda karena dipisahkan oleh rantai atau tali penghubung, sehingga untuk mempermudah dalam memahami konsep, kedua jenis hubungan roda tersebut dipisahkan.
| ||
Perlu Diingat
| ||
Jika dua roda yang bersinggungan memiliki jumlah gerigi (gigi) sebanyak nA dan nB, maka berlaku persamaan sebagai berikut:
ωA
|
=
|
RB
|
=
|
nB
|
Keterangan:
| |||
ωB
|
RA
|
nA
|
nA
|
=
|
Jumlah gigi roda A
| |||
nB
|
=
|
Jumlah gigi roda B
| ||||||
Persamaan tersebut memberi arti bahwa kecepatan sudut yang dimiliki roda-roda yang bersinggungan berbanding terbalik dengan jumlah gigi yang dimilikinya. Pernyataan ini dapat kita lihat kebenarannya saat melihat dua roda dengan jumlah gigi yang berbeda. Roda dengan jumlah gigi yang lebih banyak akan berputar lebih lambat daripada roda dengan jumlah gigi sedikit.
Contoh Soal 3
Dua buah silinder bersinggungan satu sama lain seperti pada gambar di bawah ini. Diketahui jari-jari dari masing-masing silinder sebesar RA = 50 cm dan RB = 30 cm. Kemudian silinnder B dihubungkan pada mesin penggerak sehingga dapat berputar dengan kecepatan sudut tetap 5 rad/s. Jika kedua silinder dapat berputar tanpa slip, tentukan kecepatan linear silinder A dan B serta kecepatan sudut silinder A!
Penyelesaian
RA = 50 cm = 0,5 m
RB = 30 cm = 0,3 m
ωB = 5 rad/s
Ditanya: kecepatan linear silinder A dan B serta kecepatan sudut silinder A
Dua roda dalam hal ini silinder yang saling bersinggungan memiliki kecepatan linear yang sama besar. Jadi kecepatan linear kedua silinder tersebut adalah vB = vA
Kecepatan linear silinder B
vB = ωB × RB
vB = 5 × 0,3
v1 = 1,5 m/s
Kecepatan linear silinder A
vA = vB
vA = 1,5 m/s
Kecepatan sudut silinder A
vA = ωA× RA
ωA = vA/ RA
ωA = 1,5/0,5
ωA = 3 rad/s
Demikianlah artikel tentang rumus atau persamaan hubungan roda-roda sepusat (seporos), hubungan roda-roda yang dihubungkan dengan rantai (tali) dan hubungan roda-roda yang saling bersinggungan beserta contoh soal dan pembahasannya. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.







Terima kasih sangat membantu
ReplyDeleteTerima kasih .. Jelas sekalii
ReplyDeletetrimakasih.ketemu dg psikotest yg mendasarkan pd penjelasan tsb.
ReplyDeleteMakasih ilmunya
ReplyDeleteSangat membantu, terimakasih ♡
ReplyDeleteJwjenskansbdkxmsmsksloknsnmlslksnsns jsnsnsks ksnsnnsksjncndsns
DeleteYo love me
DeleteTerimakasih, pembelajaran dikelas terbantu
ReplyDeleteCara mennentukan moment nya gimana? ?
ReplyDeletebelum sampe materi momen kak
DeleteTerimakasih, sangat membantu
ReplyDeleteJazakumullahi khairan katsiran ka��
ReplyDeleteGambarnya boleh di ambil kak untuk di upload di ig? Nanti di sertakan link nya
ReplyDeletegambarnya boLeh di upload ke ig gk kak? Nanti di sertakan link nya:) makasih kak
ReplyDelete