Cara Menentukan Vektor Resultan dengan Metode Analisis
https://www.fisikabc.com/2017/04/resultan-vektor-metode-analisis.html
Daftar Materi Fisika
Advertisement
Baca Juga:
Dalam artikel cara melukis vektor resultan dengan metode grafis, telah disinggung sedikit mengenai metode untuk menentukan vektor resultan salah satunya adalah metode analisis. Menentukan resultan vektor menggunakan metode analisis adalah cara menentukan resultan vektor melalui proses penguraian vektor menjadi vektor-vektor komponennya.
Sebelum Anda memulai materi ini, Anda harus tahu bagaimana teknik dasar dalam menguraikan vektor menjadi komponen-komponennya. Oleh karena itu, sebaiknya Anda pelajari dahulu cara mudah menguraikan vektor menjadi vektor komponennya. Atau jika Anda sudah paham, langsung saja mulai dari sini.
Apa itu Vektor Komponen?
Untuk mengetahui jawabannya, perhatikan gambar penguraian vektor berikut
Pada gambar penguraian vektor V tersebut, terdapat dua vektor proyeksi yang saling tegak lurus yaitu vektor VX yang terletak pada sumbu X bidang kartesius dan vektor VY yang terletak pada sumbu Y bidang kartesius. Kedua vektor tersebut merupakan vektor komponen dari vektor V. jadi dapat disimpulkan bahwa:
Vektor Komponen adalah hasil proyeksi suatu vektor terhadap sumbu X dan sumbu Y bidang Cartesius yang saling tegak lurus.
|
Bagaimana Cara Menjumlahkan atau Mengurangkan Vektor dengan Metode Analisis?
Di dalam menentukan besar dan juga arah vektor resultan, vektor komponen menjadi sangat penting untuk dipahami agar dalam menggambarkan vektor komponen tersebut tidak terjadi kesalahan. Karena salah menggambarkan arah saja bisa berbeda hasil resultannya.
Lalu bagaimana cara menentukan resultan hasil penjumlahan maupun pengurangan vektor dengan metode analitis? Untuk bisa menjawabnya perhatikan contoh gambar tiga buah vektor berikut.
 |
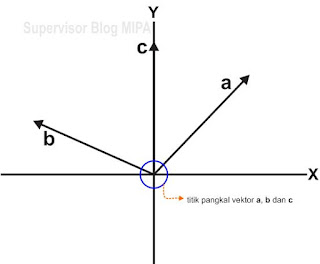
| Gambar Vektor Acuan |
#1 Penjumlahan Vektor dengan Metode Analisis
Untuk menggambarkan penjumlahan vektor dengan metode analisis, vektor harus diuraikan ke dalam komponen-komponennya, baik komponen pada sumbu X maupun Y.
Perhatikan Gambar Vektor Acuan di atas. Kita akan mencoba menggambarkan penjumlahan vektor a + b + c dengan metode analitis. Langkah-langkahnya adalah sebagai berikut:
A.Gambarlah bidang koordinat kartesius. Kemudian, gambar vektor a, b dan c pada bidang koordinat tersebut dengan pangkal masing-masing vektor berada di pusat koordinat.
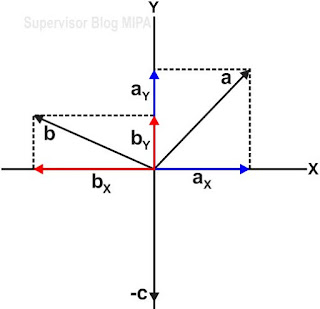
B.Uraikan/proyeksikan vektor a, b dan c ke dalam sumbu Xdan Y (aX, aY, bX, bY, cX, dan cY).
C.Karena vektor c berhimpit pada sumbu Y maka vektor c tidak memiliki vektor komponen pada sumbu X dan komponen vektor pada sumbu Y yaitu cy = c. Kemudian setelah vektor komponen terbentuk, jumlahkan semua komponen vektor pada sumbu X dan semua komponen vektor pada sumbu Y. rumusnya adalah sebagai berikut:
ΣRX = aX - bX
ΣRY = aY + bY + c
Dari kedua persamaan tersebut, besar resultan vektor dapat dicari dengan rumus:
Sedangkan arah resultan dapat dicari dengan persamaan:
#2 Pengurangan atau Selisih Vektor dengan Metode Analisis
Pengurangan atau selisih vektor menggunakan metode analisis pada prinsipnya sama dengan penjumlahan. Kalau pada pengurangan, vektor yang menjadi pengurang (tanda negatif) hanya dibalik arahnya sehingga berlawanan arah dengan vektor semula.
Perhatikan Gambar Vektor Acuan di atas. Kita akan mencoba menggambarkan pengurangan vektor a + b - c atau bisa juga ditulis dengan a + b +(- c) dengan metode analitis. Langkah-langkahnya adalah sebagai berikut:
A.Gambarlah bidang koordinat kartesius. Kemudian, gambar vektor a, b dan c pada bidang koordinat tersebut dengan pangkal masing-masing vektor berada di pusat koordinat. Jangan lupa, putar vektor c 180o sehingga menghasilkan vektor baru –c yang besarnya sama dengan vektor c tetapi dengan arah yang berlawanan.
B.Uraikan/proyeksikan vektor a dan b ke dalam sumbu Xdan Y (aX, aY, bX, dan bY). vektor -c tidak perlu diuraikan karena tidak memiliki vektor komponen pada sumbu Xsedangkan vektor komponen pada sumbu Y yaitu cY = -c.
C.Kemudian setelah vektor komponen terbentuk, jumlahkan semua komponen vektor pada sumbu X dan semua komponen vektor pada sumbu Y. rumusnya adalah sebagai berikut:
ΣRX = aX - bX
ΣRY = aY + bY – c
Untuk menentukan besar dan arah resultan hasil pengurangan dapat menggunakan rumus atau persamaan sebelumnya.
Dalam Penjumlahan dan pengurangan vektor menggunakan metode analitis di atas, untuk menentukan nilai resultan vektor secara kuantitaif (dinyatakan dengan angka) hanya bisa dilakukan melalui proses pengukuran, sama halnya dengan metode segitiga dan metode poligon.
Namun keuntungan menggunakan metode analisis dalam menentukan resultan vektor adalah kita dapat mencari nilai resultan secara kuantitaif menggunakan perhitungan berupa rumus. Dengan syarat besar vektor dan sudut yang dibentuk terhadap sumbu X atau Y sudah diketahui.
Bagaimanakah Rumus untuk Menentukan Nilai dan Arah Vektor Resultan dalam Metode Analisis?
Untuk menentukan persamaan resultan vektor dalam metode analisis, perhatikan gambar 3 buah vektor F dibawah ini.
Vektor F1, F2 dan F3 masing-masing membentuk sudut α1, α2 dan α3 terhadap sumbu X, maka vektor-vektor komponen pada sumbu X dan Y adalah sebagai berikut:
Jika nilai komponen vektor pada sumbu X dan sumbu Ysudah diketahui maka nilai vektor Resultan dapat dicari dengan rumus:
Vektor komponen pada sumbu X
|
Vektor komponen pada sumbu Y
|
F1X = F1 cos α1
|
F1Y = F1 sin α1
|
F2X = F2 cos α2
|
F2Y = F2 sin α2
|
F3X = F3 cos α3
|
F3Y = F3 sin α3
|
ΣFX = F1 cos α1 + F2 cos α2 + F3 cos α3
|
ΣFY = F1 sin α1 + F2 sin α2 + F3 sin α3
|
Secara umum, jika sebanyak n buah vektor bekerja pada satu bidang datar membentuk sudut sebanyak n buah αterhadap sumbu X, maka rumus resultan vektor komponen pada sumbu X dan Y adalah sebagai berikut:
ΣFX = F1 cos α1 + F2 cos α2 + F3 cos α3 +……...+Fn cos αn
|
ΣFY = F1 sin α1 + F2 sin α2 + F3 sin α3 +……...+Fn sin αn
|
Sedangkan arah resultan terhadap X positif (β) dapat dicari dengan rumus:
Demikianlah artikel tentang cara menentukan vektor resultan dengan metode analisis atau penguraian. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.






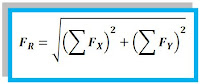

Thank you
ReplyDeleteMakasih :)
ReplyDeleteUntuk nilai sudutnya pakai sudut istimewa?
ReplyDeletebisa pake kalkulator
DeleteBpk, kenapa yang dekat dengan sudut identik dgn cos ? Dasarnya apa pak ? Bingung saya pak
ReplyDeleteItu pakai aturan trigonometri
DeleteContoh soal untuk penjumlahan vektor Secara anilitis dong ?🙏
ReplyDeleteSepertinya udah ada di blog ini
DeleteKnp utk mencari f3x memakain alfa 2, bukanya 3 ?
ReplyDeleteiya kak itu terdapat kesalahan penulisan, artikel akan segera kami perbaiki, terimakasih atas koreksinya.
Delete