Cara Mudah Menguraikan Vektor Menjadi Komponennya
https://www.fisikabc.com/2017/04/penguraian-vektor.html?m=0
Daftar Materi Fisika
Advertisement
Baca Juga:
Dalam artikel tentang sifat-sifat vektor, telah disebutkan bahwa terdapat 5 macam sifat vektor dan salah satunya adalah vektor dapat diuraikan. Lalu yang menjadi pertanyaannya sekarang adalah Apa itu penguraian vektor? Bagaimana cara menguraikan vektor? Dan untuk apa sih vektor diuraikan?
Untuk menjawab pertanyaan-pertanyaan tersebut perhatikan gambar ilutrasi berikut ini.
Namun jika ditanya lagi, mengapa dapat bergerak seperti itu? Jawabannya adalah gaya F merupakan besaran vektor. Vektor F dapat diuraikan atau diproyeksikan ke arah horizontal (FX) dan ke arah vertikal (FY). Perhatikan gambar vektor yang bekerja pada box kayu berikut ini.
Jika FY lebih kecil dibanding dengan berat box kayu dan lantai licin, maka box kayu akan bergerak searah FX yaitu ke arah horizontal ke kanan. Contoh seperti ini berlaku untuk semua vektor. Setiap vektor dapat diuraikan menjadi 2 komponen yang saling tegak lurus. Komponen-komponen penguraian vektor ini disebut juga proyeksi vektor. Berdasarkan ilustrasi tersebut dapat disimpulkan bahwa:
Penguraian Vektor adalah suatu cara menyatakan sebuah vektor dengan dua vektor lain yang saling tegak lurus dalam bidang cartesius.
Sekarang akan dibahas cara mudah dalam menguraikan vektor menjadi vektor komponennya. Langkah-langkahnya adalah sebagai berikut:
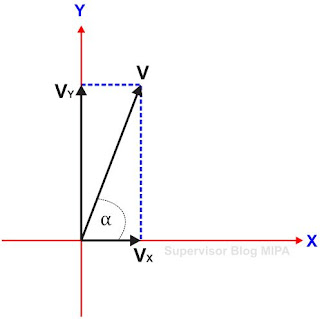
Misalkan ada gambar sebuah vektor kecepatan V seperti ini
Maka untuk menguraikan vektor kecepatan tersebut adalah
- Gambar sebuah koordinat kartesius dengan sumbu X dan sumbu Y-nya, dengan memposisikan titik tangkap vektor di titik pusat koordinat. Tuliskan juga besar sudut kemiringan vektor terhadap sumbu X (misalnya sudut α)
- Tarik garis proyeksi tegak lurus dari ujung vektor ke arah sumbu Y dan sumbu X
- Gambar dua vektor dari titik pusat koordinat menuju titik potong garis proyeksi pada sumbu X dan sumbu Y. dan beri nama masing-masing vektor dengan VX dan VY
- Selesai. Bagaimana? Sangat mudah bukan cara menguraikan vektor menjadi vektor komponennya.
Setelah Anda tahu bagaimana cara menguraikan vektor, selanjutnya Anda juga harus tahu bagaimana cara menentukan besar atau nilai vektor tersebut. Rumus mencari besar vektor dengan metode penguraian adalah dengan menerapkan Dalil Phytagoras. Persamaannya adalah sebagai berikut:
Dari gambar segitiga di atas, Anda dapat mencari panjang Vx dan Vy dengan menggunakan rumus sinus dan kosinus pada segitiga siku-siku. Dari rumus sinus dan kosinus, kita dapat mencari Vx dan Vy yaitu:
Vx = V cos α
Vy = V cos α
Keterangan:
Vx = komponen vektor pada sumbu X
Vy = komponen vektor pada sumbu Y
α = sudut yang dibentuk vektor dengan sumbu X positif.
Rumus di atas berlaku jika besar vektor V dan sudut α sudah diketahui. Bagaimana jika dibalik, yang diketahui dalam soal adalah VX dan VY? maka untuk mencari besar/nilai suatu vektor jika nilai vektor komponennya sudah diketahui adalah menggunakan rumus sebagai berikut:
Terakhir, kembali lagi ke pertanyaan di awal tadi. Untuk apa vektor di uraikan? Jawabannya sangat simpel. Fungsi vektor diuraikan adalah untuk mencari nilai resultan vektor dan juga untuk menganalisis gaya-gaya yang bekerja pada suatu benda jika benda tersebut diberikan sebuah gaya dengan sudut kemiringan tertentu.
Demikianlah artikel tetang cara menguraikan vektor menjadi vektor komponennya, rumus menghitung besar vektor komponen dan juga arah vektor. Semoga dapat bermanfaat untuk Anda. Terimakasih atas kunjungannya dan sampai jumpa di artikel berikutnya.






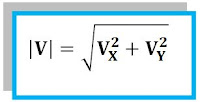

Min pada sumbu y-nya juga pake cos atau sin?
ReplyDeleteYang bener pake sin Vy = V sin α
ReplyDelete